
【题目】如图,已知△ABC是等边三角形,BD是AC上的高线.作AE⊥AB于点A,交BD的延长线于点E.取BE的中点M,连结AM.

(1)求证:△AEM是等边三角形;
(2)若AE=2,求△AEM的面积.
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:AF+EF=DE;
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
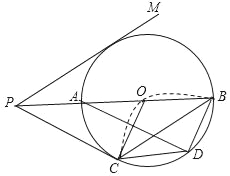
【题目】如图,AB为⊙O的直径,点C为⊙O上一点,将弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,连接OC,CD,BD,过点C的切线与线段BA的延长线交于点P,连接AD,在PB的另一侧作∠MPB=∠ADC.
(1)判断PM与⊙O的位置关系,并说明理由;
(2)若PC=![]() ,求四边形OCDB的面积.
,求四边形OCDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,求∠MNA的度数.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.求BC的长;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A,B,C在小正方形的顶点上.
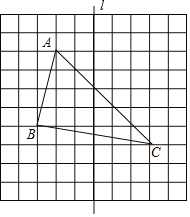
(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′
(2)三角形ABC的面积为 ;
(3)在直线l上找一点P,使PA+PB的长最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线PQ∥MN,点A在PQ上,直角△BEF的直角边BE在MN上,且∠B=90°,∠BEF=30°.现将△BEF绕点B以每秒1°的速度按逆时针方向旋转(E,F的对应点分别是E′,F′),同时,射线AQ绕点A以每秒4°的速度按顺时针方向旋转(Q的对应点是Q′).设旋转时间为t秒(0≤t≤45).
(1)∠MBF′=__.(用含t的代数式表示)
(2)在旋转的过程中,若射线AQ′与边E′F′平行时,则t的值为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
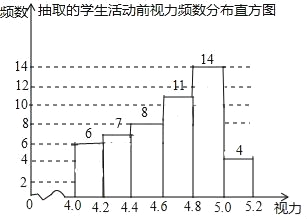
【题目】为了保护视力,某学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示,(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表格所示.
抽取的学生活动后视力频数分布表
分组 | 频数 |
4.0≤x<4.2 | 2 |
4.2≤x<4.4 | 4 |
4.4≤x<4.6 | 6 |
4.6≤x<4.8 | 10 |
4.8≤x<5.0 | 21 |
5.0≤x<5.2 | 7 |
(1)此次调查所抽取的样本容量为 ;
(2)若视力达到4.8以上(含4.8)为达标,请估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com