
【题目】如图,直线PQ∥MN,点A在PQ上,直角△BEF的直角边BE在MN上,且∠B=90°,∠BEF=30°.现将△BEF绕点B以每秒1°的速度按逆时针方向旋转(E,F的对应点分别是E′,F′),同时,射线AQ绕点A以每秒4°的速度按顺时针方向旋转(Q的对应点是Q′).设旋转时间为t秒(0≤t≤45).
(1)∠MBF′=__.(用含t的代数式表示)
(2)在旋转的过程中,若射线AQ′与边E′F′平行时,则t的值为__.

【答案】(90﹣t)°,6°或42°
【解析】
(1)如图1,由题意得:∠FBF'=t°,∠FBM=90°,根据互余的概念进行求解即可得;°;
(2)①如图2、图3,分两种情况分别画出图形进行求解即可得.
(1)如图1,由题意得:∠FBF'=t°,∠FBM=90°,
∴∠MBF'=90°﹣t°=(90﹣t)°,
故答案为:(90﹣t)°;
(2)①如图2,AQ'∥E'F',
延长BE'交AQ'于C,则∠F'E'B=∠ACB=30°,
由题意得:∠EBE'=t°,∠QAQ'=4t°,
∴t+4t=30,
t=6°;
②如图3,AQ'∥E'F',
延长BE',交PQ于D,交直线AQ'于C,则∠F'E'B=∠ACD=30°,
由题意得:∠NBE'=t°,∠QAQ'=4t°,
∴∠ADB=∠NBE'=t°,
∵∠ADB=∠ACD+∠DAC,
∴30+180﹣4t=t,
t=42°,
综上,在旋转的过程中,若射线AQ′与边E′F′平行时,则t的值为6°或42°,
故答案为:6°或42°.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )
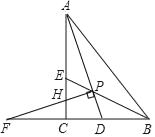
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四个完全相同的小球上分别写有:0, ![]() ,﹣5,π四个实数,把它们全部装入一个布袋里,从布袋里任意摸出1个球,球上的数是无理数的概率为 .
,﹣5,π四个实数,把它们全部装入一个布袋里,从布袋里任意摸出1个球,球上的数是无理数的概率为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察,在如图所示的各图中找对顶角(不含平角):

(1)如图a,图中共有_____对对顶角.
(2)如图b,图中共有_____对对顶角.
(3)如图c,图中共有_____对对顶角
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成多少对对顶角?
(5)若有2000条直线相交于一点,则可形成多少对对顶角?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设A:踢毽子;B:篮球:C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如两个统计图.请结合图中的信息解答下列问题:
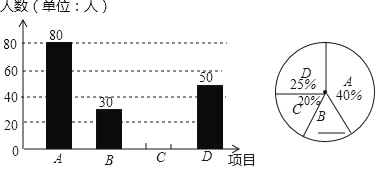
(1)本次共调查了多少名学生?
(2)请将两个统计图补充完整.
(3)求图中“A”层次所在扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元。设生产A种产品的生产件数为x, A、B两种产品所获总利润为y (元)
(1)试写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一果农贩卖的西红柿,其重量与价钱成一次函数关系.小华向果农买一竹篮的西红柿,含竹篮称得总重量为15公斤,付西红柿的钱26元,若再加买0.5公斤的西红柿,需多付1元,则空竹篮的重量为多少?( )
A. 1.5 B. 2 C. 2.5 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如题![]() ,
,![]() ,点
,点![]() 是边
是边![]() 的中点,点
的中点,点![]() 是边
是边![]() 上的一个动点,作
上的一个动点,作![]() 交
交![]() 于点
于点![]() ,
,![]() 的延长线交线段
的延长线交线段![]() 于点
于点![]() .
.
(1)如图①,当点![]() 于点
于点![]() 重合时,求证:
重合时,求证:![]() ;
;
(2)设![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数解析式,并写出定义域.
的函数解析式,并写出定义域.
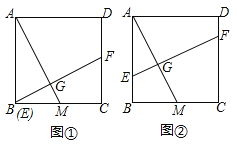
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将自然数按以下规律排列:

表中数2在第二行第一列,与有序数对(2,1)对应,数5与(1,3)对应,数14与(3,4)对应,根据这一规律,数2014对应的有序数对为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com