练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在矩形ABCD中，E，F分别是AD，BC的中点，AF与BE相交于点M，CE与DF相交于点N，QM⊥BE，QN⊥EC相交于点Q，PM⊥AF，PN⊥DF相交于点P，若2BC=3AB，记△ABM和△CDN的面积和为S，则四边形MQNP的面积为（　　）

    A. S B. S C. S D. S

    【答案】C

    【解析】

    连接EF．证明≌，设，则连接MN交EF于O，则 证明根据相似三角形的性质得到进而求出S菱形MQNP 即可求出四边形MQNP的面积

    连接EF．

    ∵四边形ABCD是矩形，

    ∴四边形ABFE，四边形CDEF都是矩形，且是全等的矩形，

    ∴

    ∵

    ∴

    连接PF，在和 中，

    ∴≌，

    ∴

    ∴E、P、F共线，同法可证，E、Q、F共线，则易证四边形MQNP是菱形，

    ∵，

    设，则连接MN交EF于O，则

    ∵

    ∴

    ∴

    ∴S菱形MQNP

    ∵和的面积和为S，

    ∴

    ∴

    ∴S菱形MQNP

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC 中，∠C=90°，∠A=34°，D，E 分别为 AB，AC 上一点，将△BCD，△ADE 沿 CD，DE 翻折，点 A，B 恰好重合于点 P 处，则∠ACP=_______________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，AB=AC，BC交⊙O于点D， AC交⊙O于点E，∠BAC=45°。

    （1）求∠EBC的度数；

    （2）求证：BD=CD。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠C＝90°，BC＝5．

    ⑴ 利用直尺和圆规在AB边上求作一点P，使得∠APC＋∠BCP＝90°，并说明理由；（不写作法，保留作图痕迹）

    ⑵ 在⑴的条件下，试判断∠PCB与∠A之间的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒，当t的值为_____秒时，△ABP和△DCE全等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长方形ABCD中，AB＝6，AD＝9，延长BC到E，使CE＝3，连接DE.动点P从点B出发，以每秒3个单位的速度沿BC→CD→DA向终点A运动，设点P运动的时间为t秒，当t为______秒时，以P、A、B三点构成的三角形和△DCE全等.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

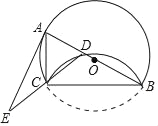
    【题目】如图，以AB为直径作⊙O，点C为⊙O上一点，劣弧CB沿BC翻折，交AB于点D，过A作⊙O的切线交DC的延长线于点E．

    （1）求证：AC=CD；

    （2）已知tanE=，AC=2，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以AB为直径作⊙O，点C为⊙O上一点，劣弧CB沿BC翻折，交AB于点D，过A作⊙O的切线交DC的延长线于点E．

    （1）求证：AC=CD；

    （2）已知tanE=，AC=2，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，正三角形ABC的边长为3＋.

    (1)如图，正方形EFPN的顶点E，F在边AB上，顶点N在边AC上，在正三角形ABC及其内部，以点A为位似中心，作正方形EFPN的位似正方形E′F′P′N′，且使正方形E′F′P′N′的面积最大(不要求写作法)；

    (2)求(1)中作出的正方形E′F′P′N′的面积．

    查看答案和解析>>

    同步练习册答案