
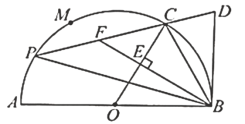
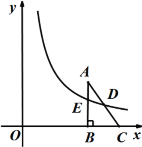
【题目】如图,![]() 为半⊙O的直径,
为半⊙O的直径,![]() ,
,![]() 是半圆上的三等分点,
是半圆上的三等分点,![]() ,
,![]() 与半⊙O相切于点
与半⊙O相切于点![]() ,点
,点![]() 为
为![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),直线
重合),直线![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,则下列结论正确的是______________.(写出所有正确结论的序号)
,则下列结论正确的是______________.(写出所有正确结论的序号)
①![]() ;②
;②![]() 的长为
的长为![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 为定值.
为定值.
【答案】②⑤
【解析】
①先根据圆的切线的性质可得![]() ,再根据半圆上的三等分点可得
,再根据半圆上的三等分点可得![]() ,然后根据圆周角定理可得
,然后根据圆周角定理可得![]() ,最后假设
,最后假设![]() ,根据角的和差、三角形的外角性质可得
,根据角的和差、三角形的外角性质可得![]() ,这与点
,这与点![]() 为
为![]() 上一动点相矛盾,由此即可得;
上一动点相矛盾,由此即可得;
②根据弧长公式即可得;
③先根据等边三角形的性质可得![]() ,再根据角的和差即可得;
,再根据角的和差即可得;
④先根据三角形的外角性质可得![]() ,从而可得对应角
,从而可得对应角![]() 与
与![]() 不可能相等,由此即可得;⑤先根据相似三角形的判定与性质可得
不可能相等,由此即可得;⑤先根据相似三角形的判定与性质可得![]() ,从而可得
,从而可得![]() ,再根据等边三角形的性质可得
,再根据等边三角形的性质可得![]() ,由此即可得.
,由此即可得.
如图,连接OP
![]() 与半⊙O相切于点
与半⊙O相切于点![]()
![]()
![]()
![]() 是半圆上的三等分点
是半圆上的三等分点
![]()
![]()
![]() 是等边三角形
是等边三角形
由圆周角定理得:![]()
假设![]() ,则
,则![]()
![]()
![]()
又![]() 点
点![]() 为
为![]() 上一动点
上一动点
![]() 不是一个定值,与
不是一个定值,与![]() 相矛盾
相矛盾
即PB与PD不一定相等,结论①错误
![]()
![]()
则![]() 的长为
的长为![]() ,结论②正确
,结论②正确
![]() 是等边三角形,
是等边三角形,![]()
![]()
![]() ,则结论③错误
,则结论③错误
![]() ,即对应角
,即对应角![]() 与
与![]() 不可能相等
不可能相等
![]() 与
与![]() 不相似,则结论④错误
不相似,则结论④错误
在![]() 和
和![]() 中,
中,![]()
![]()
![]() ,即
,即![]()
又![]() 是等边三角形,
是等边三角形,![]()
![]()
![]()
即![]() 为定值,结论⑤正确
为定值,结论⑤正确
综上,结论正确的是②⑤
故答案为:②⑤.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图所示的一次函数关系.随着补贴数额的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足![]()
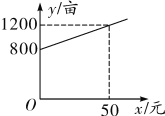
(1)求出政府补贴政策实施后,种植亩数y与政府补贴数额x之间的函数关系式;
(2)在政府出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?求出总收益w的最大值;
(4)该市希望这种蔬菜的总收益不低于7200000元,请你帮助该市确定每亩补贴数额的范围,在此条件下要使总收益最大,并说明每亩补贴数额应定为多少元合适?
参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是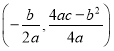 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交![]() 于点D,以OC为半径的
于点D,以OC为半径的![]() 交OA于点E,则图中阴影部分的面积是( )
交OA于点E,则图中阴影部分的面积是( )

A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC,∠ABC=90°,顶点A在第一象限,B、C在x轴的正半轴上(C在B的右侧),BC=3,AB=4,若双曲线![]() 交边AB于点E,交边AC于中点D.
交边AB于点E,交边AC于中点D.
(1)若OB=2,求k;
(2)若AE=![]() , 求直线AC的解析式.
, 求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是____________(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,过点D作BD垂线交BC的延长线于点E,且
,过点D作BD垂线交BC的延长线于点E,且![]() ,证明:四边形
,证明:四边形![]() 是垂等四边形.
是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为24的垂等四边形![]() 内接于⊙O中,
内接于⊙O中,![]() .求⊙O的半径.
.求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是甘肃省博物馆的镇馆之宝——铜奔马,又称“马踏飞燕”,于1969年10月出土于武威市的雷台汉墓,1983年10月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有“马踏飞燕”雕塑,某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:
课题 | 测量“马踏飞燕”雕塑最高点离地面的高度 | |||
测量示意图 |
| 如图,雕塑的最高点 | ||
测量数据 |
|
|
| 仪器 |
|
| 5米 |
| |
请你根据上表中的测量数据,帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
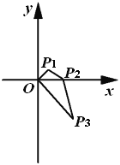
【题目】如图,在平面直角坐标系中,点![]() 的坐标
的坐标 ,将线段
,将线段![]() 绕点
绕点![]() 按顺时针方向旋转45°,再将其长度伸长为
按顺时针方向旋转45°,再将其长度伸长为![]() 的2倍,得到线段
的2倍,得到线段![]() ;又将线段
;又将线段![]() 绕点
绕点![]() 按顺时针方向旋转45°,长度伸长为
按顺时针方向旋转45°,长度伸长为![]() 的2倍,得到线段
的2倍,得到线段![]() ;如此下去,得到线段
;如此下去,得到线段![]() 、
、![]() ,……,
,……,![]() (
(![]() 为正整数),则点
为正整数),则点![]() 的坐标是_________.
的坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
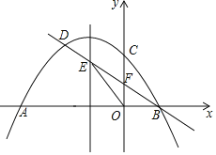
【题目】如图,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点B的直线与抛物线的另一个交点为D,与抛物线的对称轴交于点E,与y轴交于点F,且
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点B的直线与抛物线的另一个交点为D,与抛物线的对称轴交于点E,与y轴交于点F,且![]() ,△OBE的面积为
,△OBE的面积为![]() .
.
(1)求抛物线的解析式;
(2)设P为已知抛物线上的任意一点,当△ACP的面积等于△ACB的面积时,求点P的坐标;
(3)点Q(0,m)是y轴上的动点,连接AQ、BQ,当∠AQB为钝角时,则m的取值范围是 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假期里,小红和小惠去买菜,三次购买的西红柿价格和数量如下表:
单价/(元/千克) | 4 | 3 | 2 | 合计 |
小红购买的数量/千克 | 1 | 2 | 3 | 6 |
小惠购买的数量/千克 | 2 | 2 | 2 | 6 |
(1)小红和小惠购买西红柿数量的中位数、众数是多少?
(2)从平均价格看,谁买的西红柿要便宜些.请思考下面小亮和小明的说法,你认为谁说得对?为什么?
小亮的说法
每次购买单价相同,购买总量也相同,平均价格应该也一样,都是![]() (元/千克),所以两人购买的西红柿一样便宜.
(元/千克),所以两人购买的西红柿一样便宜.
小明的说法
购买的总量虽然相同,但小红花了16元,小惠花了18元,平均价格不一样,所以小红购买的西红柿便宜.
(3)小明在直角坐标系中画出反比例函数的图象,图象经过点![]() (如图),点
(如图),点![]() 的横、纵坐标分别为小红和小惠购买西红柿价格的平均数.
的横、纵坐标分别为小红和小惠购买西红柿价格的平均数.
①求此反比例函数的关系式;
②判断点![]() 是否在此函数图象上.
是否在此函数图象上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com