
【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图所示的一次函数关系.随着补贴数额的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足![]()
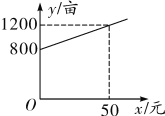
(1)求出政府补贴政策实施后,种植亩数y与政府补贴数额x之间的函数关系式;
(2)在政府出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?求出总收益w的最大值;
(4)该市希望这种蔬菜的总收益不低于7200000元,请你帮助该市确定每亩补贴数额的范围,在此条件下要使总收益最大,并说明每亩补贴数额应定为多少元合适?
参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是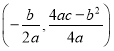 .
.
【答案】(1)![]() ;(2)2400000元;(3)政府应将每亩补贴数额定为450元,总收益w的最大值是7260000元;(4)每亩补贴数额应定为400元到500元最合适
;(2)2400000元;(3)政府应将每亩补贴数额定为450元,总收益w的最大值是7260000元;(4)每亩补贴数额应定为400元到500元最合适
【解析】
(1)设种植亩数y与政府补贴数额x之间的函数关系式是![]() ,
,
由图象过![]() ,将两点代入得:
,将两点代入得:
![]() ,
,
解得:![]() ,
,
∴![]() .
.
答:政府补贴政策实施后,种植亩数y与政府补贴数额x之间的函数关系式是![]() ;
;
(2)![]() ,
,
当![]() 时,
时,![]() ,
,
总收益为![]() 元.
元.
答:在政府出台补贴措施前,该市种植这种蔬菜的总收益额为2400000元;
(3)![]() ,
,
∵![]() ,对称轴
,对称轴![]() ,
,
∴当![]() 时,
时,
![]()
![]() (元),
(元),
∴当x定为450元时,总收益达到最大值,最大值为7260000元.
答:要使全市这种蔬菜的总收益w最大,政府应将每亩补贴数额定为450元,总收益w的最大值是7260000元;
(4)![]() ,
,
∴![]() .
.
因此,定为400元到500元.
答:每亩补贴数额应定为400元到500元最合适.


科目:初中数学 来源: 题型:
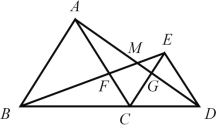
【题目】如图所示,![]() 均为等边三角形,边长分别为
均为等边三角形,边长分别为![]() ,B、C、D三点在同一条直线上,则下列结论正确的________________.(填序号)
,B、C、D三点在同一条直线上,则下列结论正确的________________.(填序号)
①![]() ②
②![]() ③
③![]() 为等边三角形 ④
为等边三角形 ④![]() ⑤CM平分
⑤CM平分![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
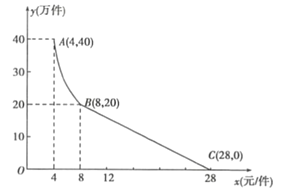
【题目】“净扬”水净化有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的小型水净化产品,已于当年投入生产并进行销售.已知生产这种小型水净化产品的成本为4元/件,在销售过程中发现:每年的年销售量![]() (万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种水净化产品的年利润z(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值;
(3)假设公司的这种水净化产品第一年恰好按年利润z(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种水净化产品每件的销售价格x(元)定在8元以上(![]() ),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,
,![]() ,
,![]() ,直线
,直线![]() 是抛物线的对称轴,在直线
是抛物线的对称轴,在直线![]() 右侧的抛物线上有一动点
右侧的抛物线上有一动点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
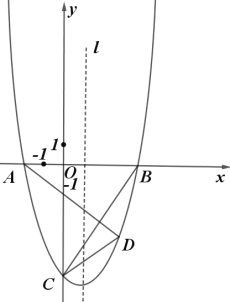
(1)求抛物线的函数表达式;
(2)若点![]() 在
在![]() 轴的下方,当
轴的下方,当![]() 的面积是
的面积是![]() 时,求
时,求![]() 的面积;
的面积;
(3)在(2)的条件下,点![]() 是
是![]() 轴上一点,点
轴上一点,点![]() 是抛物线上一动点,是否存在点
是抛物线上一动点,是否存在点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点,以
为顶点,以![]() 为一边的四边形是平行四边形,若存在,求出点
为一边的四边形是平行四边形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送.若两车合作,各运12趟才能完成,需支付运费共4800元;若甲、乙两车单独运完此堆垃圾,则乙车所运趟数是甲车的2倍;已知乙车每趟运费比甲车少200元.
探究:
(1)分别求出甲、乙两车每趟的运费;
(2)若单独租用甲车运完此堆垃圾,需运多少趟;
发现:若同时租用甲、乙两车,则甲车运x趟,乙车运y趟,才能运完此堆垃圾,其中![]() 均为正整数.
均为正整数.
(1)当![]() 时,
时,![]() ______;当
______;当![]() 时,
时,![]() ______;
______;
(2)求y与x之间满足的函数关系式.
决策:在“发现”的条件下,设总运费为w(元).
(1)求w与x之间满足的函数关系式,当x取何值时,w取得最小值;
(2)当![]() 且
且![]() 时,甲车每趟的运费打7折,乙车每趟的运费打9折,当x取何值时,w取得最小值.
时,甲车每趟的运费打7折,乙车每趟的运费打9折,当x取何值时,w取得最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个边长都为![]() 的小正方形组成的网格中,小正方形的顶点叫做格点.线段
的小正方形组成的网格中,小正方形的顶点叫做格点.线段![]() 的端点
的端点![]() 均在格点上.
均在格点上.
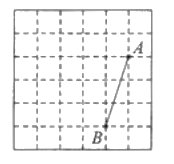
(1)线段![]() 的长度等于 ;
的长度等于 ;
(2)将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,在图中画出
,在图中画出![]() ,并连结
,并连结![]() .
.
(3)在线段![]() 上确定一点
上确定一点![]() 连结
连结![]() ,使得
,使得![]() 与
与![]() 的面积比为
的面积比为![]() .
.
说明:以上作图只用无刻度的直尺画图,保留画图痕迹,不写画法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随州市新水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD.
(1)求最短的斜拉索DE的长;
(2)求最长的斜拉索AC的长.
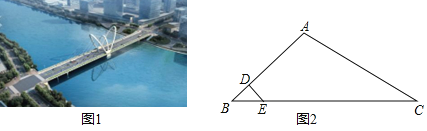
查看答案和解析>>
科目:初中数学 来源: 题型:
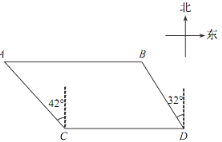
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的木栈道 AB ,栈道 AB 与景区道路CD 平行.在 C 处测得栈道一端 A 位于北偏西 42°方向,在 D 处测得栈道另一端 B 位于北偏西 32°方向.已知 CD =120 m , BD =80 m ,求木栈道 AB 的长度(结果保留整数) .
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
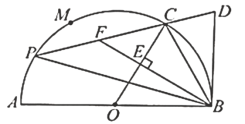
【题目】如图,![]() 为半⊙O的直径,
为半⊙O的直径,![]() ,
,![]() 是半圆上的三等分点,
是半圆上的三等分点,![]() ,
,![]() 与半⊙O相切于点
与半⊙O相切于点![]() ,点
,点![]() 为
为![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),直线
重合),直线![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,则下列结论正确的是______________.(写出所有正确结论的序号)
,则下列结论正确的是______________.(写出所有正确结论的序号)
①![]() ;②
;②![]() 的长为
的长为![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com