
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送.若两车合作,各运12趟才能完成,需支付运费共4800元;若甲、乙两车单独运完此堆垃圾,则乙车所运趟数是甲车的2倍;已知乙车每趟运费比甲车少200元.
探究:
(1)分别求出甲、乙两车每趟的运费;
(2)若单独租用甲车运完此堆垃圾,需运多少趟;
发现:若同时租用甲、乙两车,则甲车运x趟,乙车运y趟,才能运完此堆垃圾,其中![]() 均为正整数.
均为正整数.
(1)当![]() 时,
时,![]() ______;当
______;当![]() 时,
时,![]() ______;
______;
(2)求y与x之间满足的函数关系式.
决策:在“发现”的条件下,设总运费为w(元).
(1)求w与x之间满足的函数关系式,当x取何值时,w取得最小值;
(2)当![]() 且
且![]() 时,甲车每趟的运费打7折,乙车每趟的运费打9折,当x取何值时,w取得最小值.
时,甲车每趟的运费打7折,乙车每趟的运费打9折,当x取何值时,w取得最小值.
【答案】探究:(1)甲、乙两车每趟的运费分别为300元、100元;(2)单独租用甲车运完此堆垃圾,需运18趟发现:(1)16,13;(2)![]() ;决策:(1)当
;决策:(1)当![]() 时,w有最小值,w的最小值为3700元;(2)当
时,w有最小值,w的最小值为3700元;(2)当![]() 时,w有最小值,w的最小值为3540元.
时,w有最小值,w的最小值为3540元.
【解析】
探究:(1)设甲、乙两车每趟的运费分别为m元、n元,
由题意得![]() ,
,
解得:![]() ;
;
答:甲、乙两车每趟的运费分别为300元、100元.
(2)设单独租用甲车运完此堆垃圾,需运a趟,由题意得
![]() ,
,
解得![]() ,
,
经检验![]() 是原方程的解.
是原方程的解.
答:单独租用甲车运完此堆垃圾,需运18趟.
发现:(1)16,13.
【解法提示】由题意得:![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(2)∵![]() ,
,
∴![]() ;
;
决策:(1)![]()
![]()
![]() (
(![]() ,且x为正整数),
,且x为正整数),
∵![]() ,∴y随x的增大而增大,
,∴y随x的增大而增大,
∴当![]() 时,w有最小值,w的最小值为3700元.
时,w有最小值,w的最小值为3700元.
(2)![]()
![]()
![]() ,
,
∵![]() 且
且![]() ,即
,即![]() ,
,
∴![]() ,且x为正整数,
,且x为正整数,
∴当![]() 时,w有最小值,w的最小值为3540元.
时,w有最小值,w的最小值为3540元.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某农户要改造部分农田种植蔬菜.经调查,平均每亩改造费用是900元,添加辅助设备费用(元)与改造面积(亩)的平方成正比,比例系数为18,以上两项费用三年内不需再投入;每亩种植蔬菜还需种子、人工费用600元,这项费用每年均需再投入,除上述费用外,没有其他费用,设改造![]() 亩,每亩蔬菜年销售额为
亩,每亩蔬菜年销售额为![]() 元.
元.
(1)设改造当年收益为![]() 元,用含
元,用含![]() ,
,![]() 的式子表示
的式子表示![]() ;
;
(2)按前三年计算,若![]() ,是否改造面积越大收益越大?改造面积为多少时,可以得到最大收益?
,是否改造面积越大收益越大?改造面积为多少时,可以得到最大收益?
(3)若![]() ,按前三年计算,能确保改造的面积越大收益也越大,求
,按前三年计算,能确保改造的面积越大收益也越大,求![]() 的取值范围.
的取值范围.
注:收益=销售额-(改造费+辅助设备费+种子、人工费).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:A:![]() ;B:
;B:![]() ;C:
;C:![]() ;D:
;D:![]() ,并绘制出如下不完整的统计图.
,并绘制出如下不完整的统计图.

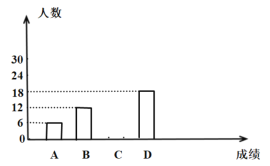
(1)求被抽取的学生成绩在C:![]() 组的有多少人;
组的有多少人;
(2)所抽取学生成绩的中位数落在哪个组内;
(3)若该学校有![]() 名学生,估计这次竞赛成绩在A:
名学生,估计这次竞赛成绩在A:![]() 组的学生有多少人.
组的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知点A为x轴上的一动点,其坐标为(m,0)点B的坐标为(![]() ,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C,
,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C,![]() 关于直线
关于直线![]() 对称,
对称,![]() 交直线
交直线![]() 于点E若△BOE的面积为4,则点E的坐标为________
于点E若△BOE的面积为4,则点E的坐标为________
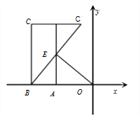
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图所示的一次函数关系.随着补贴数额的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足![]()
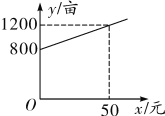
(1)求出政府补贴政策实施后,种植亩数y与政府补贴数额x之间的函数关系式;
(2)在政府出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?求出总收益w的最大值;
(4)该市希望这种蔬菜的总收益不低于7200000元,请你帮助该市确定每亩补贴数额的范围,在此条件下要使总收益最大,并说明每亩补贴数额应定为多少元合适?
参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是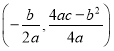 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,水平桌面上有甲、乙、丙三个圆柱形容器,它们的高都为![]() 且甲、丙容器的底面积相同,乙容器在距离底部
且甲、丙容器的底面积相同,乙容器在距离底部![]() 高度处与甲、丙容器连通(联通处的体积忽略不计).甲容器中有水,水位高为
高度处与甲、丙容器连通(联通处的体积忽略不计).甲容器中有水,水位高为![]() .若用水管向乙容器中匀速注水,直至三个容器都注满水,乙容器中的水位
.若用水管向乙容器中匀速注水,直至三个容器都注满水,乙容器中的水位![]() 与注水时间
与注水时间![]() 之间的函数图象如图②所示.
之间的函数图象如图②所示.
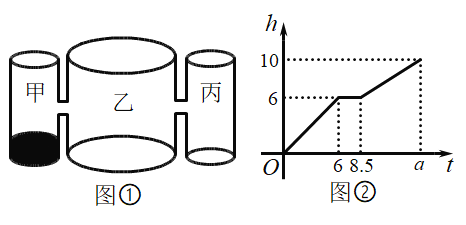
(1)甲、乙两容器的底面积之比为 ;
(2)图②中![]() 的值为 ;
的值为 ;
(3)若将注水管改为向容器丙中匀速注水,且注水速度不变,请在图③中画出容器丙中水位![]() 与注水时间
与注水时间![]() 之间的函数图象.
之间的函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李莉在五张完全相同并且没有任何标记的卡片的一面分别写下数据﹣4,﹣1,0,3,5,将写有数据的一面朝下放置,并混合均匀.
(1)随机摸起一张,求上面的数据为负数的概率;
(2)随机摸起两张,其中一张表示x,另一张表示y,求点(x,y)在直线y=﹣x﹣1上的概率;
(3)随机摸起一张,记为x,然后放回,混合均匀后再随机摸起一张,记为y,求点(x,y)是第四象限内的点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是____________(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,过点D作BD垂线交BC的延长线于点E,且
,过点D作BD垂线交BC的延长线于点E,且![]() ,证明:四边形
,证明:四边形![]() 是垂等四边形.
是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为24的垂等四边形![]() 内接于⊙O中,
内接于⊙O中,![]() .求⊙O的半径.
.求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com