
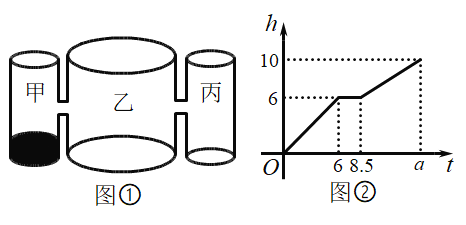
【题目】如图①,水平桌面上有甲、乙、丙三个圆柱形容器,它们的高都为![]() 且甲、丙容器的底面积相同,乙容器在距离底部
且甲、丙容器的底面积相同,乙容器在距离底部![]() 高度处与甲、丙容器连通(联通处的体积忽略不计).甲容器中有水,水位高为
高度处与甲、丙容器连通(联通处的体积忽略不计).甲容器中有水,水位高为![]() .若用水管向乙容器中匀速注水,直至三个容器都注满水,乙容器中的水位
.若用水管向乙容器中匀速注水,直至三个容器都注满水,乙容器中的水位![]() 与注水时间
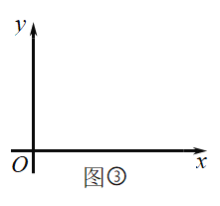
与注水时间![]() 之间的函数图象如图②所示.
之间的函数图象如图②所示.
(1)甲、乙两容器的底面积之比为 ;
(2)图②中![]() 的值为 ;
的值为 ;
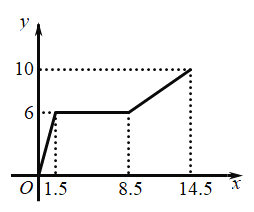
(3)若将注水管改为向容器丙中匀速注水,且注水速度不变,请在图③中画出容器丙中水位![]() 与注水时间
与注水时间![]() 之间的函数图象.
之间的函数图象.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)如图所示见解析.
;(3)如图所示见解析.
【解析】
(1)观察图象即可知:单独加水到乙容器6cm处要6分钟,然后再将甲丙加水到题意高度用了2.5分钟,由匀速注水列方程即可解决问题;
(2)根据容器总体积除以每分钟加水体积即可解答;
(3)根据题意先加水丙到6cm,再加加到6cm,再加甲到6cm处,最后一同加满,由此计算即可画出图像.
解:(1)设甲容器底面积为s,甲乙容器的底面积之比为k,依题意得:
![]() ,解得:
,解得:![]() ,
,
故答案为:![]() ;
;
(2)设甲容器底面积为s,所以需加水体积为:![]() ,
,
加水速度为![]() ,
,
∴加水总时间为:![]() (秒)
(秒)
故答案为:![]() ;
;
(3)如图所示:
0
由(2)可知丙容器加至6cm处所需时间为:![]() (秒),
(秒),
甲乙容器加至6cm处所需时间为:![]() (秒),此时丙容器高度不变,即到8.5秒时高度为6cm不变,
(秒),此时丙容器高度不变,即到8.5秒时高度为6cm不变,
最后加满容器由(2)可知加水总时间为![]() 秒.
秒.
故图象如图所示.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴,y轴交于点A,B两点,点C为OB的中点,抛物线
分别与x轴,y轴交于点A,B两点,点C为OB的中点,抛物线![]() 经过A,C两点.
经过A,C两点.

(1)求抛物线的函数表达式;
(2)点D是直线AB下方的抛物线上的一点,且![]() 的面积为
的面积为![]() ,求点D的坐标;
,求点D的坐标;
(3)点P为抛物线上一点,若![]() 是以AB为直角边的直角三角形,求点P到抛物线的对称轴的距离.
是以AB为直角边的直角三角形,求点P到抛物线的对称轴的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送.若两车合作,各运12趟才能完成,需支付运费共4800元;若甲、乙两车单独运完此堆垃圾,则乙车所运趟数是甲车的2倍;已知乙车每趟运费比甲车少200元.
探究:
(1)分别求出甲、乙两车每趟的运费;
(2)若单独租用甲车运完此堆垃圾,需运多少趟;
发现:若同时租用甲、乙两车,则甲车运x趟,乙车运y趟,才能运完此堆垃圾,其中![]() 均为正整数.
均为正整数.
(1)当![]() 时,
时,![]() ______;当
______;当![]() 时,
时,![]() ______;
______;
(2)求y与x之间满足的函数关系式.
决策:在“发现”的条件下,设总运费为w(元).
(1)求w与x之间满足的函数关系式,当x取何值时,w取得最小值;
(2)当![]() 且
且![]() 时,甲车每趟的运费打7折,乙车每趟的运费打9折,当x取何值时,w取得最小值.
时,甲车每趟的运费打7折,乙车每趟的运费打9折,当x取何值时,w取得最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC内一点,BD⊥CD,E、F、G、H分别是边AB、BD、CD、AC的中点.若AD=10,BD=8,CD=6,则四边形EFGH的周长是( )
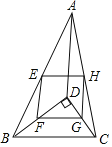
A.24B.20C.12D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随州市新水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD.
(1)求最短的斜拉索DE的长;
(2)求最长的斜拉索AC的长.
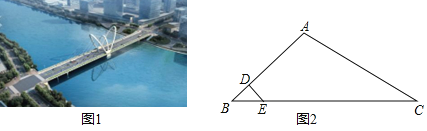
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区超市一段时间每天订购80个面包进行销售,每售出1个面包获利润0.5元,未售出的每个亏损0.3元.(1)若今后每天售出的面包个数用x(0<x≤80)表示,每天销售面包的利润用y(元)表示,写出y与x的函数关系式;
(2)小明连续m天对该超市的面包销量进行统计,并制成了频数分别直方图(每个组距包含左边的数,但不包含右边的数)和扇形统计图,如图1、图2所示,请结合两图提供的信息,解答下列问题:
①m的值为 ;
②求在m天内日销售利润少于32元的天数;
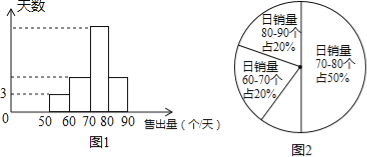
(3)如图(2)中m天内日销售面包个数在70≤x<80这个组内的销售情况如表:
销售量/个 | 70 | 72 | 73 | 75 | 78 | 79 |
天数 | 1 | 2 | 3 | 4 | 3 | 2 |
请计算该组内平均每天销售面包的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AC为直径的⊙O恰为△ABC的外接圆,∠ABC的平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AB=25,BC=![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com