
【题目】随州市新水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD.
(1)求最短的斜拉索DE的长;
(2)求最长的斜拉索AC的长.
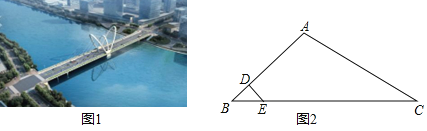
【答案】(1)最短的斜拉索DE的长为3![]() m;(2)最长的斜拉索AC的长为30m.
m;(2)最长的斜拉索AC的长为30m.
【解析】(1)根据等腰直角三角形的性质计算DE的长;
(2)作AH⊥BC于H,如图2,由于BD=DE=3![]() ,则AB=3BD=15
,则AB=3BD=15![]() ,在Rt△ABH中,根据等腰直角三角形的性质可计算出BH=AH=15,然后在Rt△ACH中利用含30度的直角三角形三边的关系即可得到AC的长.
,在Rt△ABH中,根据等腰直角三角形的性质可计算出BH=AH=15,然后在Rt△ACH中利用含30度的直角三角形三边的关系即可得到AC的长.
(1)∵∠ABC=∠DEB=45°,
∴△BDE为等腰直角三角形,
∴DE=![]() BE=
BE=![]() ×6=3
×6=3![]() ,
,
答:最短的斜拉索DE的长为3![]() m;
m;
(2)作AH⊥BC于H,如图2,
∵BD=DE=3![]() ,
,
∴AB=3BD=5×3![]() =15
=15![]() ,
,
在Rt△ABH中,∵∠B=45°,
∴BH=AH=![]() AB=
AB=![]() ×15
×15![]() =15,
=15,
在Rt△ACH中,∵∠C=30°,
∴AC=2AH=30.
答:最长的斜拉索AC的长为30m.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
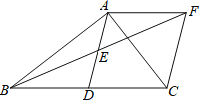
【题目】如图,在![]() ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:![]() AEF≌△DEB;
AEF≌△DEB;
(2)若∠BAC=90°,求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:A:![]() ;B:
;B:![]() ;C:
;C:![]() ;D:
;D:![]() ,并绘制出如下不完整的统计图.
,并绘制出如下不完整的统计图.

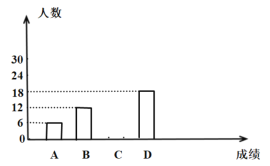
(1)求被抽取的学生成绩在C:![]() 组的有多少人;
组的有多少人;
(2)所抽取学生成绩的中位数落在哪个组内;
(3)若该学校有![]() 名学生,估计这次竞赛成绩在A:
名学生,估计这次竞赛成绩在A:![]() 组的学生有多少人.
组的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图所示的一次函数关系.随着补贴数额的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足![]()
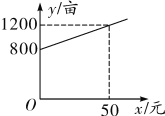
(1)求出政府补贴政策实施后,种植亩数y与政府补贴数额x之间的函数关系式;
(2)在政府出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?求出总收益w的最大值;
(4)该市希望这种蔬菜的总收益不低于7200000元,请你帮助该市确定每亩补贴数额的范围,在此条件下要使总收益最大,并说明每亩补贴数额应定为多少元合适?
参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是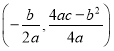 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,水平桌面上有甲、乙、丙三个圆柱形容器,它们的高都为![]() 且甲、丙容器的底面积相同,乙容器在距离底部
且甲、丙容器的底面积相同,乙容器在距离底部![]() 高度处与甲、丙容器连通(联通处的体积忽略不计).甲容器中有水,水位高为
高度处与甲、丙容器连通(联通处的体积忽略不计).甲容器中有水,水位高为![]() .若用水管向乙容器中匀速注水,直至三个容器都注满水,乙容器中的水位
.若用水管向乙容器中匀速注水,直至三个容器都注满水,乙容器中的水位![]() 与注水时间
与注水时间![]() 之间的函数图象如图②所示.
之间的函数图象如图②所示.
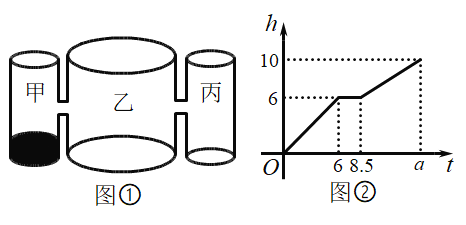
(1)甲、乙两容器的底面积之比为 ;
(2)图②中![]() 的值为 ;
的值为 ;
(3)若将注水管改为向容器丙中匀速注水,且注水速度不变,请在图③中画出容器丙中水位![]() 与注水时间
与注水时间![]() 之间的函数图象.
之间的函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂将![]() 四种型号的空调销售额的情况绘制成了图①和图②两幅尚不完整的统计图.
四种型号的空调销售额的情况绘制成了图①和图②两幅尚不完整的统计图.
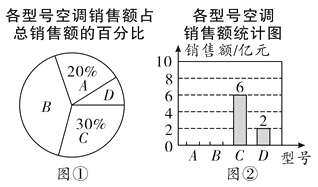
(1)请补全图②的条形统计图;
(2)为了应对激烈的市场竞争,该厂决定降价促销,![]() 四种型号的空调分别降价
四种型号的空调分别降价![]() ,因此该厂宣称其产品平均降价
,因此该厂宣称其产品平均降价![]() ,你认为该厂的说法正确吗?请通过计算说明理由;
,你认为该厂的说法正确吗?请通过计算说明理由;
(3)为进一步促销,该厂决定从这四种型号的空调中任意选取两种型号的空调降价销售,请用树状图或列表法求出降价空调中含D型号空调的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李莉在五张完全相同并且没有任何标记的卡片的一面分别写下数据﹣4,﹣1,0,3,5,将写有数据的一面朝下放置,并混合均匀.
(1)随机摸起一张,求上面的数据为负数的概率;
(2)随机摸起两张,其中一张表示x,另一张表示y,求点(x,y)在直线y=﹣x﹣1上的概率;
(3)随机摸起一张,记为x,然后放回,混合均匀后再随机摸起一张,记为y,求点(x,y)是第四象限内的点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交![]() 于点D,以OC为半径的
于点D,以OC为半径的![]() 交OA于点E,则图中阴影部分的面积是( )
交OA于点E,则图中阴影部分的面积是( )

A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
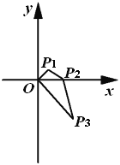
【题目】如图,在平面直角坐标系中,点![]() 的坐标
的坐标 ,将线段
,将线段![]() 绕点
绕点![]() 按顺时针方向旋转45°,再将其长度伸长为
按顺时针方向旋转45°,再将其长度伸长为![]() 的2倍,得到线段
的2倍,得到线段![]() ;又将线段
;又将线段![]() 绕点
绕点![]() 按顺时针方向旋转45°,长度伸长为
按顺时针方向旋转45°,长度伸长为![]() 的2倍,得到线段
的2倍,得到线段![]() ;如此下去,得到线段
;如此下去,得到线段![]() 、
、![]() ,……,
,……,![]() (
(![]() 为正整数),则点
为正整数),则点![]() 的坐标是_________.
的坐标是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com