
【题目】某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:A:![]() ;B:
;B:![]() ;C:
;C:![]() ;D:
;D:![]() ,并绘制出如下不完整的统计图.
,并绘制出如下不完整的统计图.

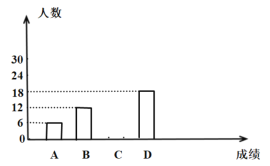
(1)求被抽取的学生成绩在C:![]() 组的有多少人;
组的有多少人;
(2)所抽取学生成绩的中位数落在哪个组内;
(3)若该学校有![]() 名学生,估计这次竞赛成绩在A:
名学生,估计这次竞赛成绩在A:![]() 组的学生有多少人.
组的学生有多少人.
【答案】(1)24人;(2)C组;(3)150人.
【解析】
(1)根据扇形统计图的B组所占比例,条形统计图得B在人数,用总人数减去A,B,D人数,可得C组人数;
(2)根据总人数多少,结合中位数的概念确定即可;
(3)根据样本中A组所占比例,用总人数乘以比例,即可得到答案.
(1)由图可知:B组人数为12;B组所占的百分比为20%,
∴本次抽取的总人数为:![]() (人),
(人),
∴抽取的学生成绩在C:![]() 组的人数为:
组的人数为:![]() (人);
(人);
(2)∵总人数为60人,
∴中位数为第30,31个人成绩的平均数,
∵![]() ,且
,且![]()
∴中位数落在C组;
(3)本次调查中竞赛成绩在A:![]() 组的学生的频率为:
组的学生的频率为:![]() ,
,
故该学校有![]() 名学生中竞赛成绩在A:
名学生中竞赛成绩在A:![]() 组的学生人数有:
组的学生人数有:![]() (人).
(人).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,点E为□ABCD对角线AC上的一点,点F在线段BE的延长线上,且EF=BE,线段EF与边CD相交于点G.
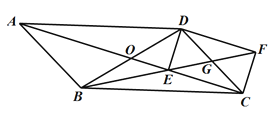
(1)求证:DF//AC;
(2)如果AB=BE,DG=CG,联结DE、CF,求证:四边形DECF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
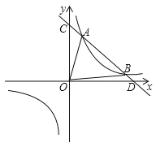
【题目】如图,已知一次函数y1=﹣x+a与x轴、y轴分别交于点D、C两点和反比例函数![]() 交于A、B两点,且点A的坐标是(1,3),点B的坐标是(3,m)
交于A、B两点,且点A的坐标是(1,3),点B的坐标是(3,m)
(1)求a,k,m的值;
(2)求C、D两点的坐标,并求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
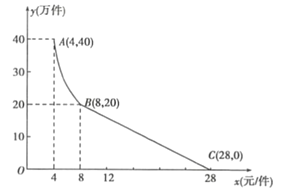
【题目】“净扬”水净化有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的小型水净化产品,已于当年投入生产并进行销售.已知生产这种小型水净化产品的成本为4元/件,在销售过程中发现:每年的年销售量![]() (万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种水净化产品的年利润z(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值;
(3)假设公司的这种水净化产品第一年恰好按年利润z(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种水净化产品每件的销售价格x(元)定在8元以上(![]() ),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,
,![]() ,
,![]() ,直线
,直线![]() 是抛物线的对称轴,在直线
是抛物线的对称轴,在直线![]() 右侧的抛物线上有一动点
右侧的抛物线上有一动点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
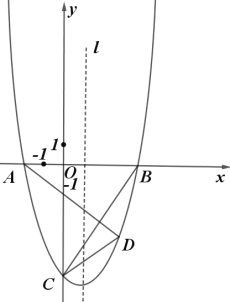
(1)求抛物线的函数表达式;
(2)若点![]() 在
在![]() 轴的下方,当
轴的下方,当![]() 的面积是
的面积是![]() 时,求
时,求![]() 的面积;
的面积;
(3)在(2)的条件下,点![]() 是
是![]() 轴上一点,点
轴上一点,点![]() 是抛物线上一动点,是否存在点
是抛物线上一动点,是否存在点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点,以
为顶点,以![]() 为一边的四边形是平行四边形,若存在,求出点
为一边的四边形是平行四边形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送.若两车合作,各运12趟才能完成,需支付运费共4800元;若甲、乙两车单独运完此堆垃圾,则乙车所运趟数是甲车的2倍;已知乙车每趟运费比甲车少200元.
探究:
(1)分别求出甲、乙两车每趟的运费;
(2)若单独租用甲车运完此堆垃圾,需运多少趟;
发现:若同时租用甲、乙两车,则甲车运x趟,乙车运y趟,才能运完此堆垃圾,其中![]() 均为正整数.
均为正整数.
(1)当![]() 时,
时,![]() ______;当
______;当![]() 时,
时,![]() ______;
______;
(2)求y与x之间满足的函数关系式.
决策:在“发现”的条件下,设总运费为w(元).
(1)求w与x之间满足的函数关系式,当x取何值时,w取得最小值;
(2)当![]() 且
且![]() 时,甲车每趟的运费打7折,乙车每趟的运费打9折,当x取何值时,w取得最小值.
时,甲车每趟的运费打7折,乙车每趟的运费打9折,当x取何值时,w取得最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随州市新水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD.
(1)求最短的斜拉索DE的长;
(2)求最长的斜拉索AC的长.
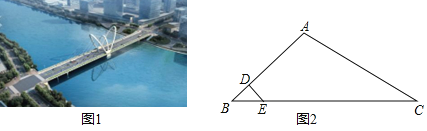
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春天来了,石头城边,秦淮河畔,鸟语花香,柳条飘逸.为给市民提供更好的休闲锻炼环境,决定对一段总长为1800米的外秦淮河沿河步行道出新改造,该任务由甲、乙两工程队先后接力完成.甲工程队每天改造12米,乙工程队每天改造8米,共用时200天.
(1)根据题意,小莉、小刚两名同学分别列出尚不完整的方程组如下:
小莉:![]() 小刚:
小刚:
根据两名同学所列的方程组,请你分别指出未知数x、y表示的意义,然后在方框中补全小莉、小刚两名同学所列的方程组:
小莉:x表示 ,y表示 ;
小刚:x表示 ,y表示 .
(2)求甲、乙两工程队分别出新改造步行道多少米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com