
【题目】已知:如图,点E为□ABCD对角线AC上的一点,点F在线段BE的延长线上,且EF=BE,线段EF与边CD相交于点G.
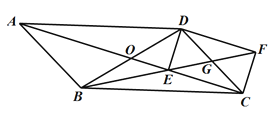
(1)求证:DF//AC;
(2)如果AB=BE,DG=CG,联结DE、CF,求证:四边形DECF是矩形.
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.
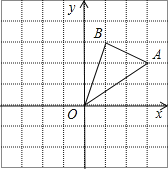
(1)点A关于点O中心对称的点的坐标为 ;
(2)点A1的坐标为 ;
(3)在旋转过程中,求线段AB扫过的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为奖励在家自主学习有突出表现的学生,决定购买笔记本和钢笔作为奖品.已知1本笔记本和4支钢笔共需100元,4本笔记本和6支钢笔共需190元.
(1)分别求一本笔记本和一支钢笔的售价;
(2)若学校准备购进这两种奖品共90份,并且笔记本的数量不多于钢笔数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随点
的位置随点![]() 的位置变化而变化.
的位置变化而变化.
(1)如图1,当点![]() 在菱形
在菱形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
(2)当点![]() 在菱形
在菱形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车沿同一公路从A地出发前往路程为100千米的B地,乙车比甲车晚出发15分钟,行驶过程中所行驶的路程分别用y1、y2(千米)表示,它们与甲车行驶的时间x(分钟)之间的函数关系如图所示.
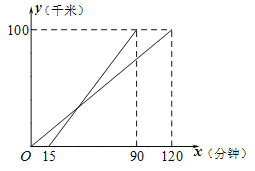
(1)分别求出y1、y2关于x的函数解析式并写出定义域;
(2)乙车行驶多长时间追上甲车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某剧场第一排座位分布图:甲、乙、丙、丁四人购票,所购票分别为2,3,4,5.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位之和最小.如果按“甲、乙、丙、丁”的先后顺序购票,那么甲甲购买1,2号座位的票,乙购买3,5,7号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序______.

查看答案和解析>>
科目:初中数学 来源: 题型:
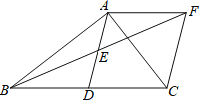
【题目】如图,在![]() ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:![]() AEF≌△DEB;
AEF≌△DEB;
(2)若∠BAC=90°,求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:A:![]() ;B:
;B:![]() ;C:
;C:![]() ;D:
;D:![]() ,并绘制出如下不完整的统计图.
,并绘制出如下不完整的统计图.

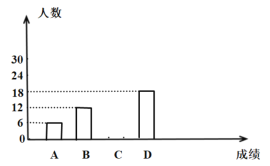
(1)求被抽取的学生成绩在C:![]() 组的有多少人;
组的有多少人;
(2)所抽取学生成绩的中位数落在哪个组内;
(3)若该学校有![]() 名学生,估计这次竞赛成绩在A:
名学生,估计这次竞赛成绩在A:![]() 组的学生有多少人.
组的学生有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com