
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随点
的位置随点![]() 的位置变化而变化.
的位置变化而变化.
(1)如图1,当点![]() 在菱形
在菱形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
(2)当点![]() 在菱形
在菱形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.

【答案】(1)BP=CE; CE⊥AD;(2)成立,理由见解析;(3)![]() .
.
【解析】(1)①连接AC,证明△ABP≌△ACE,根据全等三角形的对应边相等即可证得BP=CE;②根据菱形对角线平分对角可得![]() ,再根据△ABP≌△ACE,可得
,再根据△ABP≌△ACE,可得![]() ,继而可推导得出
,继而可推导得出![]() ,即可证得CE⊥AD;
,即可证得CE⊥AD;
(2)(1)中的结论:BP=CE,CE⊥AD 仍然成立,利用(1)的方法进行证明即可;
(3)连接AC交BD于点O,CE,作EH⊥AP于H,由已知先求得BD=6,再利用勾股定理求出CE的长,AP长,由△APE是等边三角形,求得![]() ,
, ![]() 的长,再根据
的长,再根据![]() ,进行计算即可得.
,进行计算即可得.
(1)①BP=CE,理由如下:
连接AC,
∵菱形ABCD,∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE ,∠PAE=60° ,
∴∠BAP=∠CAE,
∴△ABP≌△ACE,∴BP=CE;
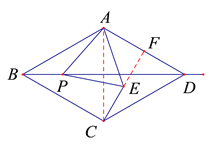
②CE⊥AD ,
∵菱形对角线平分对角,
∴![]() ,
,
∵△ABP≌△ACE,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴CF⊥AD ,即CE⊥AD;
(2)(1)中的结论:BP=CE,CE⊥AD 仍然成立,理由如下:
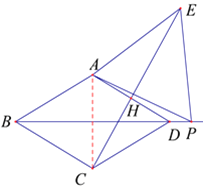
连接AC,
∵菱形ABCD,∠ABC=60°,
∴△ABC和△ACD都是等边三角形,
∴AB=AC,∠BAD=120° ,
∠BAP=120°+∠DAP,
∵△APE是等边三角形,
∴AP=AE , ∠PAE=60° ,
∴∠CAE=60°+60°+∠DAP=120°+∠DAP,
∴∠BAP=∠CAE,
∴△ABP≌△ACE,∴BP=CE,![]() ,
,
∴∠DCE=30° ,∵∠ADC=60°,
∴∠DCE+∠ADC=90° , ∴∠CHD=90° ,∴CE⊥AD,
∴(1)中的结论:BP=CE,CE⊥AD 仍然成立;
(3) 连接AC交BD于点O,CE,作EH⊥AP
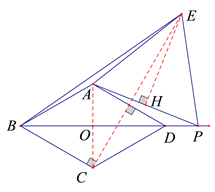
∵四边形ABCD是菱形,
∴AC⊥BD,BD平分∠ABC ,
∵∠ABC=60°,![]() ,
,
∴∠ABO=30° ,∴![]() , BO=DO=3,
, BO=DO=3,
∴BD=6,
由(2)知CE⊥AD,
∵AD∥BC,∴CE⊥BC,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
由(2)知BP=CE=8,∴DP=2,∴OP=5,
∴![]() ,
,
∵△APE是等边三角形,∴![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
=![]()
=![]()
=![]() ,
,
∴四边形ADPE的面积是![]() .
.


科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,我市城区四校决定联合购买一批足球运动装备.市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打七折.
(1)求每套队服和每个足球的价格分别是多少元?
(2)若城区四校联合购买100套队服和a(a>10)个足球,请用含a的代数式分别表示出到甲商场和乙商场购买装备所花费用;
(3)在(2)的条件下,当a=65时,你认为到甲、乙哪家商场购买比较合算?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每一幅图中都有若干个大小不同的四边形,第1幅图中有1个四边形,第2幅图中有3个四边形,第3幅图中有5个四边形…

(1)第4幅图中有 个四边形,第5幅图中有 个四边形;
(2)根据第1幅图到第5幅图的规律,推测第![]() 幅图中有 个四边形;(用含字母
幅图中有 个四边形;(用含字母![]() 的代数式表示)
的代数式表示)
(3)如果第![]() 幅图中有4039个四边形,请你计算
幅图中有4039个四边形,请你计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】概念学习
规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.
从三角形![]() 不是等腰三角形
不是等腰三角形![]() 一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
理解概念
![]() 如图1,在
如图1,在![]() 中,
中,![]() ,
,![]() ,请写出图中两对“等角三角形”
,请写出图中两对“等角三角形”![]() 概念应用
概念应用
![]() 如图2,在
如图2,在![]() 中,CD为角平分线,
中,CD为角平分线,![]() ,
,![]() .
.
求证:CD为![]() 的等角分割线.
的等角分割线.
![]() 在
在![]() 中,
中,![]() ,CD是
,CD是![]() 的等角分割线,直接写出
的等角分割线,直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为1,![]() ,
,![]() ,则有下列结论:①
,则有下列结论:①![]() ;②点C到EF的距离是2-1;③
;②点C到EF的距离是2-1;③![]() 的周长为2;④
的周长为2;④![]() ,其中正确的结论有( )
,其中正确的结论有( )
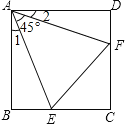
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
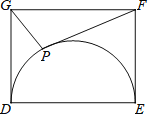
A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
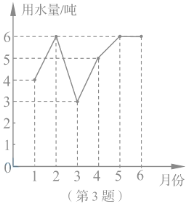
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD为正方形,点E,F分别在AB与BC上,且∠EDF=45°,易证:AE+CF=EF(不用证明).
(1)如图②,在四边形ABCD中,∠ADC=120°,DA=DC,∠DAB=∠BCD=90°,点E,F分别在AB与BC上,且∠EDF=60°.猜想AE,CF与EF之间的数量关系,并证明你的猜想;
(2)如图③,在四边形ABCD中,∠ADC=2α,DA=DC,∠DAB与∠BCD互补,点E,F分别在AB与BC上,且∠EDF=α,请直接写出AE,CF与EF之间的数量关系,不用证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com