
ЁОЬтФПЁПИХФюбЇЯА
ЙцЖЈЃКШчЙћвЛИіШ§НЧаЮЕФШ§ИіНЧЗжБ№ЕШгкСэвЛИіШ§НЧаЮЕФШ§ИіНЧЃЌФЧУДГЦетСНИіШ§НЧаЮЛЅЮЊЁАЕШНЧШ§НЧаЮЁБЃЎ
ДгШ§НЧаЮ![]() ВЛЪЧЕШбќШ§НЧаЮ
ВЛЪЧЕШбќШ§НЧаЮ![]() вЛИіЖЅЕув§ГівЛЬѕЩфЯпгыЖдБпЯрНЛЃЌЖЅЕугыНЛЕужЎМфЕФЯпЖЮАбетИіШ§НЧаЮЗжИюГЩСНИіаЁШ§НЧаЮЃЌШчЙћЗжЕУЕФСНИіаЁШ§НЧаЮжавЛИіЮЊЕШбќШ§НЧаЮЃЌСэвЛИігыдРДШ§НЧаЮЪЧЁАЕШНЧШ§НЧаЮЁБЃЌЮвУЧАбетЬѕЯпЖЮНазіетИіШ§НЧаЮЕФЁАЕШНЧЗжИюЯпЁБЃЎ
вЛИіЖЅЕув§ГівЛЬѕЩфЯпгыЖдБпЯрНЛЃЌЖЅЕугыНЛЕужЎМфЕФЯпЖЮАбетИіШ§НЧаЮЗжИюГЩСНИіаЁШ§НЧаЮЃЌШчЙћЗжЕУЕФСНИіаЁШ§НЧаЮжавЛИіЮЊЕШбќШ§НЧаЮЃЌСэвЛИігыдРДШ§НЧаЮЪЧЁАЕШНЧШ§НЧаЮЁБЃЌЮвУЧАбетЬѕЯпЖЮНазіетИіШ§НЧаЮЕФЁАЕШНЧЗжИюЯпЁБЃЎ
РэНтИХФю
![]() ШчЭМ1ЃЌдк
ШчЭМ1ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧыаДГіЭМжаСНЖдЁАЕШНЧШ§НЧаЮЁБ
ЃЌЧыаДГіЭМжаСНЖдЁАЕШНЧШ§НЧаЮЁБ![]() ИХФюгІгУ
ИХФюгІгУ
![]() ШчЭМ2ЃЌдк
ШчЭМ2ЃЌдк![]() жаЃЌCDЮЊНЧЦНЗжЯпЃЌ
жаЃЌCDЮЊНЧЦНЗжЯпЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЧѓжЄЃКCDЮЊ![]() ЕФЕШНЧЗжИюЯпЃЎ
ЕФЕШНЧЗжИюЯпЃЎ
![]() дк
дк![]() жаЃЌ
жаЃЌ![]() ЃЌCDЪЧ
ЃЌCDЪЧ![]() ЕФЕШНЧЗжИюЯпЃЌжБНгаДГі
ЕФЕШНЧЗжИюЯпЃЌжБНгаДГі![]() ЕФЖШЪ§ЃЎ
ЕФЖШЪ§ЃЎ
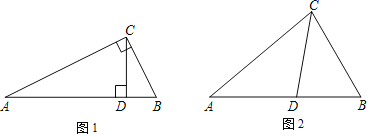
ЁОД№АИЁПЃЈ1ЃЉЁїABCгыЁїACDЃЌЁїABCгыЁїBCDЃЌЁїACDгыЁїBCDЪЧЁАЕШНЧШ§НЧаЮЁБЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЁЯACBЕФЖШЪ§ЮЊ111ЁуЛђ84ЁуЛђ106ЁуЛђ92Ёу
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЁАЕШНЧШ§НЧаЮЁБЕФЖЈвхНтД№ЃЛ
ЃЈ2ЃЉИљОнШ§НЧаЮФкНЧКЭЖЈРэЧѓГіЁЯACBЃЌИљОнНЧЦНЗжЯпЕФЖЈвхЕУЕНЁЯACDЃНЁЯDCBЃН![]()
ЁЯACBЃН40ЁуЃЌИљОнЁАЕШНЧШ§НЧаЮЁБЕФЖЈвхжЄУїЃЛ
ЃЈ3ЃЉЗжЁїACDЪЧЕШбќШ§НЧаЮЃЌDAЃНDCЁЂDAЃНACКЭЁїBCDЪЧЕШбќШ§НЧаЮЃЌDBЃНBCЁЂDCЃНBDЫФжжЧщПіЃЌИљОнЕШбќШ§НЧаЮЕФаджЪЁЂШ§НЧаЮФкНЧКЭЖЈРэМЦЫуЃЎ
ЃЈ1ЃЉЁїABCгыЁїACDЃЌЁїABCгыЁїBCDЃЌЁїACDгыЁїBCDЪЧЁАЕШНЧШ§НЧаЮЁБЃЛ
ЃЈ2ЃЉЁпдкЁїABCжаЃЌЁЯA=40ЁуЃЌЁЯB=60Ёу
ЁрЁЯACB=180Ёу-ЁЯA-ЁЯB=80Ёу
ЁпCDЮЊНЧЦНЗжЯпЃЌ
ЁрЁЯACD=ЁЯDCB= 40ЁуЃЌ
ЁрЁЯACD=ЁЯAЃЌЁЯDCB=ЁЯAЃЌ
ЁрCD=DAЃЌ
ЁпдкЁїDBCжаЃЌЁЯDCB=40ЁуЃЌЁЯB=60ЁуЃЌ
ЁрЁЯBDC=180Ёу-ЁЯDCB-ЁЯB=80ЁуЃЌ
ЁрЁЯBDC=ЁЯACBЃЌ
ЁпCD=DAЃЌЁЯBDC=ЁЯACBЃЌЁЯDCB=ЁЯAЃЌ
ЁЯB=ЁЯBЃЌ
ЁрCDЮЊЁїABCЕФЕШНЧЗжИюЯпЃЛ
ЃЈ3ЃЉЁЯACBЕФЖШЪ§ЮЊ111ЁуЛђ84ЁуЛђ106ЁуЛђ92Ёу


 ГЌФмбЇЕфгІгУЬтЬтПЈЯЕСаД№АИ
ГЌФмбЇЕфгІгУЬтЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСНИіДѓаЁВЛЭЌЕФЕШбќжБНЧШ§НЧаЮШ§НЧАхШчЭМ![]() ЫљЪОЗХжУЃЌЭМ
ЫљЪОЗХжУЃЌЭМ![]() ЪЧгЩЫќГщЯѓГіЕФМИКЮЭМаЮЃЌBЃЌCЃЌEдкЭЌвЛЬѕжБЯпЩЯЃЌСЊНсDCЃЌ
ЪЧгЩЫќГщЯѓГіЕФМИКЮЭМаЮЃЌBЃЌCЃЌEдкЭЌвЛЬѕжБЯпЩЯЃЌСЊНсDCЃЌ
![]() ЧыевГіЭМ
ЧыевГіЭМ![]() жаЕФШЋЕШШ§НЧаЮЃЌВЂИјгшЫЕУї
жаЕФШЋЕШШ§НЧаЮЃЌВЂИјгшЫЕУї![]() ЫЕУїЃКНсТлжаВЛЕУКЌгаЮДБъЪЖЕФзжФИ
ЫЕУїЃКНсТлжаВЛЕУКЌгаЮДБъЪЖЕФзжФИ![]() ЃЛ
ЃЛ
![]() ЪдЫЕУїЃК
ЪдЫЕУїЃК![]() ЃЎ
ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСРэНтЃК
Р§ЃКвбжЊЃК ![]() ЃЌ
ЃЌ
ЧѓЃК ![]() КЭ
КЭ ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
НтЃК![]()
![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
НтОіЮЪЬтЃК
ЃЈ1ЃЉШє ![]() ЃЌЧѓ xЁЂy ЕФжЕЃЛ
ЃЌЧѓ xЁЂy ЕФжЕЃЛ
ЃЈ2ЃЉвбжЊ ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ ![]() ЕФШ§БпГЄЧвТњзу
ЕФШ§БпГЄЧвТњзу ![]() ЃЌ
ЃЌ
ЂйжБНгаДГіa=__________ЃЎb=___________ЃЎ
ЂкШє![]() ЪЧ
ЪЧ ![]() жазюЖЬБпЕФБпГЄЃЈМДc<aЃЛc<bЃЉЃЌЧв
жазюЖЬБпЕФБпГЄЃЈМДc<aЃЛc<bЃЉЃЌЧв ![]() ЮЊећЪ§ЃЌжБНгаДГі
ЮЊећЪ§ЃЌжБНгаДГі ![]() ЕФжЕПЩФмЪЧ ЃЎ
ЕФжЕПЩФмЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаМЦЫуе§ШЗЕФЪЧЃЈ ЃЉ
A.ЃЈЉx3ЃЉ2=x5
B.ЃЈЉ3x2ЃЉ2=6x4
C.ЃЈЉxЃЉЉ2= ![]()
D.x8ЁТx4=x2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯBACЕФЦНЗжЯпНЛBCгкЕуDЃЌDEЁЭADЃЌНЛABгкЕуEЃЌAEЮЊЁбOЕФжБОЖ 
ЃЈ1ЃЉХаЖЯBCгыЁбOЕФЮЛжУЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁїABDЁзЁїDBEЃЛ
ЃЈ3ЃЉШєcosB= ![]() ЃЌAE=4ЃЌЧѓCDЃЎ
ЃЌAE=4ЃЌЧѓCDЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
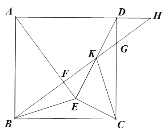
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮ![]() жаЃЌвд
жаЃЌвд![]() ЮЊбќЯђе§ЗНаЮФкВПзїЕШбќ
ЮЊбќЯђе§ЗНаЮФкВПзїЕШбќ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЎСЌНг
ЃЎСЌНг![]() ВЂбгГЄЃЌгы
ВЂбгГЄЃЌгы![]() НЛгкЕу
НЛгкЕу![]() ЃЌ гы
ЃЌ гы![]() бгГЄЯпНЛгкЕу
бгГЄЯпНЛгкЕу![]() ЃЎСЌНг
ЃЎСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎШє
ЃЎШє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ______ЃЎ
______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
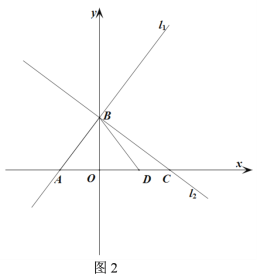
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() ЃК
ЃК![]() гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌжБЯп
гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌжБЯп![]() гыxжсЁЂyжсЗжБ№НЛгкCЁЂ
гыxжсЁЂyжсЗжБ№НЛгкCЁЂ![]() СНЕуЃЌЧв
СНЕуЃЌЧв![]() ЉU
ЉU![]() ЉU
ЉU![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжБЯп![]() ЕФНтЮіЪНЃЌВЂХаЖЯ
ЕФНтЮіЪНЃЌВЂХаЖЯ![]() ЕФаЮзДЃЛ
ЕФаЮзДЃЛ
ЃЈ2ЃЉШчЭМ![]() ЃЌ
ЃЌ![]() ЮЊжБЯп
ЮЊжБЯп![]() ЩЯвЛЕуЃЌКсзјБъЮЊ
ЩЯвЛЕуЃЌКсзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЮЊжБЯп
ЮЊжБЯп![]() ЩЯвЛЖЏЕуЃЌЕБ
ЩЯвЛЖЏЕуЃЌЕБ![]() зюаЁЪБЃЌНЋЯпЖЮ
зюаЁЪБЃЌНЋЯпЖЮ![]() биЩфЯп
биЩфЯп![]() ЗНЯђЦНвЦЃЌЦНвЦКѓ
ЗНЯђЦНвЦЃЌЦНвЦКѓ![]() ЁЂ
ЁЂ![]() ЕФЖдгІЕуЗжБ№ЮЊ
ЕФЖдгІЕуЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌЕБ
ЃЌЕБ![]() зюаЁЪБЃЌЧѓЕу
зюаЁЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ![]() ЃЌНЋ
ЃЌНЋ![]() бизХ
бизХ![]() жсЗелЃЌЕУЕН
жсЗелЃЌЕУЕН![]() ЃЌдйНЋ
ЃЌдйНЋ![]() ШЦзХЕу
ШЦзХЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЃЈ
ЃЈ![]() ЃЉЕУЕН
ЃЉЕУЕН![]() ЃЌжБЯп
ЃЌжБЯп![]() гыжБЯп
гыжБЯп![]() ЁЂ
ЁЂ![]() жсЗжБ№НЛгкЕу
жсЗжБ№НЛгкЕу![]() ЁЂ
ЁЂ![]() ЃЎЕБ
ЃЎЕБ![]() ЮЊЕШбќШ§НЧаЮЪБЃЌЧыжБНгаДГіЯпЖЮ
ЮЊЕШбќШ§НЧаЮЪБЃЌЧыжБНгаДГіЯпЖЮ![]() ЕФГЄЃЎ
ЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбвЛИізуЧђДЙжБЫЎЦНЕиУцЯђЩЯЬпЃЌЪБМфЮЊtЃЈУыЃЉЪБИУзуЧђОрРыЕиУцЕФИпЖШhЃЈУзЃЉЪЪгУЙЋЪНh=20tЉ5t2ЃЈ0ЁмtЁм4ЃЉЃЎ
ЃЈ1ЃЉЕБt=3ЪБЃЌЧѓзуЧђОрРыЕиУцЕФИпЖШЃЛ
ЃЈ2ЃЉЕБзуЧђОрРыЕиУцЕФИпЖШЮЊ10УзЪБЃЌЧѓtЃЛ
ЃЈ3ЃЉШєДцдкЪЕЪ§t1 ЃЌ t2ЃЈt1Ёйt2ЃЉЕБt=t1Лђt2ЪБЃЌзуЧђОрРыЕиУцЕФИпЖШЖМЮЊmЃЈУзЃЉЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
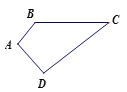
ЁОЬтФПЁПвбжЊдкЫФБпаЮABCDжаЃЌЁЯA=90ЁуЃЌAB=3ЃЌAD=4ЃЌBC=12ЃЌCD=13ЃЌЧѓЫФБпаЮABCDЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com