
【题目】如图,在正方形![]() 中,以
中,以![]() 为腰向正方形内部作等腰
为腰向正方形内部作等腰![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .连接
.连接![]() 并延长,与
并延长,与![]() 交于点
交于点![]() , 与
, 与![]() 延长线交于点
延长线交于点![]() .连接
.连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,则
,则![]() ______.
______.
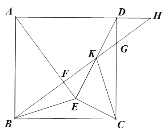
【答案】![]()
【解析】
设DG=3a,CG=9a,作KM⊥CD于M,EN⊥AB于N,想办法求出线段KF、EF、KM、EN、FG,想办法用a的代数式表示四边形EFKC的面积,再求出a即可解决问题;
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAD=∠ADC=90°,
∵CG=3DG,
∴可以假设DG=3a,CG=9a,
则AB=AD=BC=CD=12a,
∴DG∥AB,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴DH=4a,GH=5a,BH=20a,
∵AE2=BFBH,AE=AB,
∴AB2=BFBH,
∴![]() =
=![]() ,∵∠ABF=∠ABH,
,∵∠ABF=∠ABH,
∴△ABF∽HBA,
∴∠AFB=∠BAH=90°,
∴AF=![]() =
=![]() a,BF=
a,BF=![]() a,
a,
∴FG=BH-BF-GH=![]() a,
a,
∵AE=AD,
∴∠ADE=∠AED,
∵∠ADE+∠GDK=90°,∠KEF+∠EKF=90°,∠EKF=∠GKD,
∴∠GDK=∠GKD,
∴GD=GK=3a,
作KM⊥CD于M,EN⊥AB于N,

∵![]() =
=![]() ,
,
∴KM=![]() a,
a,
∵△AFB≌△ANE,
∴EN=BF=![]() a,
a,
∴S四边形EFKC=S△EFK+S△ECK
=s△EFK+(S△CDE-S△CDK)
=![]() ×
×![]() a×
a×![]() a+(
a+(![]() ×12a×
×12a×![]() a-
a-![]() ×12a×
×12a×![]() a)
a)
=![]() a2,
a2,
∵FG=![]() a=
a=![]() ,
,
∴a=![]() ,
,
∴S四边形EFKC=![]() ,
,
故答案为![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,若∠BAC=100°,则∠EAG=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,点E是AB边上一点.
(1)BF⊥CE于点F,交CD于点G(如图①).求证:AE=CG;
(2)AH⊥CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF. 
(1)求证:△ABE≌△EGF;
(2)若AB=2,S△ABE=2S△ECF , 求BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】概念学习
规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.
从三角形![]() 不是等腰三角形
不是等腰三角形![]() 一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
理解概念
![]() 如图1,在
如图1,在![]() 中,
中,![]() ,
,![]() ,请写出图中两对“等角三角形”
,请写出图中两对“等角三角形”![]() 概念应用
概念应用
![]() 如图2,在
如图2,在![]() 中,CD为角平分线,
中,CD为角平分线,![]() ,
,![]() .
.
求证:CD为![]() 的等角分割线.
的等角分割线.
![]() 在
在![]() 中,
中,![]() ,CD是
,CD是![]() 的等角分割线,直接写出
的等角分割线,直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一淘宝店主购进![]() 、
、![]() 两款
两款![]() 恤在网上进行销售,
恤在网上进行销售,![]() 款
款![]() 恤每件价格
恤每件价格![]() 元,
元,![]() 款
款![]() 恤每件价格
恤每件价格![]() 元,第一批共购买
元,第一批共购买![]() 件.
件.
(1)该淘宝店主第一批购进的![]() 恤的总费用不超过
恤的总费用不超过![]() 元,求
元,求![]() 款
款![]() 恤最少购买多少件?
恤最少购买多少件?
(2)由于销售情况良好,该淘宝店主打算购进第二批![]() 恤,购进的
恤,购进的![]() 、
、![]() 两款
两款![]() 恤件数之比为
恤件数之比为![]() ,价格保持第一批的价格不变;第三批购进
,价格保持第一批的价格不变;第三批购进![]() 款
款![]() 恤的价格在第一批购买的价格上每件减少了
恤的价格在第一批购买的价格上每件减少了![]() 元,
元,![]() 款
款![]() 恤的价格比第一批购进的价格上每件增加了
恤的价格比第一批购进的价格上每件增加了![]() 元,
元,![]() 款
款![]() 恤的数量比第二批增加了
恤的数量比第二批增加了![]() ,
,![]() 款
款![]() 恤的数量比第二批减少了
恤的数量比第二批减少了![]() ,第二批与第三批购进的
,第二批与第三批购进的![]() 恤的总费用相同,求
恤的总费用相同,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠A=∠C,点P在边AB上. 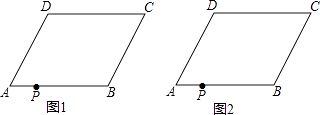
(1)判断四边形ABCD的形状并加以证明;
(2)若AB=AD,以过点P的直线为轴,将四边形ABCD折叠,使点B、C分别落在点B′、C′上,且B′C′经过点D,折痕与四边形的另一交点为Q.
①在图2中作出四边形PB′C′Q(保留作图痕迹,不必说明作法和理由);
②如果∠C=60°,那么 ![]() 为何值时,B′P⊥AB.
为何值时,B′P⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,若点P能落在线段AB上,则线段CF长的最小值是_____.
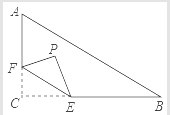
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及平行四边形ABDC的面积![]() .
.
(2)在y轴上是否存在一点P,连接PA,PB,使![]() =2
=2![]() ,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
(3)点P是四边形ABCD边上的点,若△OPC为等腰三角形时,直接写出点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com