
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����A=��C����P�ڱ�AB�ϣ� 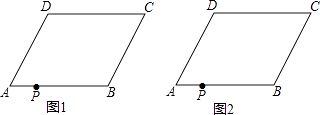
��1���ж��ı���ABCD����״������֤����
��2����AB=AD���Թ���P��ֱ��Ϊ�ᣬ���ı���ABCD�۵���ʹ��B��C�ֱ����ڵ�B�䡢C���ϣ���B��C�侭����D���ۺ����ı��ε���һ����ΪQ��
����ͼ2�������ı���PB��C��Q��������ͼ�ۼ�������˵�����������ɣ���
�������C=60�㣬��ô ![]() Ϊ��ֵʱ��B��P��AB��
Ϊ��ֵʱ��B��P��AB��
���𰸡�
��1���⣺�ı���ABCD��ƽ���ı���
֤���������ı���ABCD�У�AD��BC��
���A+��B=180�㣬
�ߡ�A=��C��
���C+��B=180�㣬
��AB��CD��
���ı���ABCD��ƽ���ı���
��2���⣺����ͼ���£�

�ڵ�AB=ADʱ��ƽ���ı���ABCD�����Σ�
���۵��ɵã�BP=B��P��CQ=C��Q��BC=B��C�䣬��C=��C��=60��=��A��
��B��P��ABʱ����B��P��C��Q���ɵ�C��Q��CD��
���PEA=30��=��DEB�䣬��QDC��=30��=��B��DE��
��B��D=B��E��
��AP=a��BP=b����ֱ��������APE�У�PE= ![]() a����B��P=b��BC=B��C��=CD=a+b��
a����B��P=b��BC=B��C��=CD=a+b��
��B��E=b�� ![]() a=B��D��
a=B��D��
��C��D=a+b����b�� ![]() a��=a+
a��=a+ ![]() a��
a��
��ֱ��������C��QD�У�C��Q= ![]() a=CQ��DQ=
a=CQ��DQ= ![]() C��Q=
C��Q= ![]() a��
a��
��CD=DQ+CQ=a+b��
�� ![]() a+
a+ ![]() a=a+b��
a=a+b��
�����ã� ![]() +1��a=b��
+1��a=b��
�� ![]() =
= ![]() =
= ![]() ����
���� ![]() =
= ![]()
����������1����������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��ν����жϣ���2���ٸ�����ԳƵ����ʽ�����ͼ���ɣ����ȸ����۵��ó�һЩ��Ӧ����ȣ���Ӧ����ȣ����Ƶ���B��D=B��E������AP=a��BP=b�����ý�ֱ�������ν�DQ��CQ���ú�a�Ĵ���ʽ��ʾ������������CD=DQ+CQ�г�����a��b�Ĺ�ϵʽ�����a��b�ı�ֵ���ɣ�������Ҫ������ƽ���ı����Լ����Σ�����Ĺؼ�������ƽ���ı��ε��ж��Լ����ε��ж������ʣ��ڽ���ʱע�⣬���ε������߶���ȣ��������۵������У���Ҫץס��Ӧ����ȣ���Ӧ�������Щ������ϵ���۵������ʵ������ԳƵ����ʣ�


 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CD�ǡ�O��ֱ������֪��1=30�㣬���2=�� �� 
A.30��
B.45��
C.60��
D.70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.����x3��2=x5
B.����3x2��2=6x4
C.����x����2= ![]()
D.x8��x4=x2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �У���
�У���![]() Ϊ�����������ڲ�������
Ϊ�����������ڲ�������![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ������
������![]() ���ӳ�����
���ӳ�����![]() ���ڵ�
���ڵ�![]() �� ��
�� ��![]() �ӳ��߽��ڵ�
�ӳ��߽��ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ����
����![]() ��
��![]() ����
����![]() ______��
______��
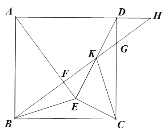
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() ��x�ᡢy��ֱ���A��B���㣬ֱ��
��x�ᡢy��ֱ���A��B���㣬ֱ��![]() ��x�ᡢy��ֱ���C��
��x�ᡢy��ֱ���C��![]() ���㣬��
���㣬��![]() �U
�U![]() �U
�U![]() ��
��
��1����ֱ��![]() �Ľ���ʽ�����ж�
�Ľ���ʽ�����ж�![]() ����״��
����״��
��2����ͼ![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬������Ϊ
��һ�㣬������Ϊ![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() ��һ���㣬��
��һ���㣬��![]() ��Сʱ�����߶�
��Сʱ�����߶�![]() ������
������![]() ����ƽ�ƣ�ƽ�ƺ�
����ƽ�ƣ�ƽ�ƺ�![]() ��
��![]() �Ķ�Ӧ��ֱ�Ϊ
�Ķ�Ӧ��ֱ�Ϊ![]() ��
��![]() ����
����![]() ��Сʱ�����
��Сʱ�����![]() �����ꣻ
�����ꣻ
��3����ͼ![]() ����
����![]() ����
����![]() �ᷭ�ۣ��õ�
�ᷭ�ۣ��õ�![]() ���ٽ�
���ٽ�![]() ���ŵ�
���ŵ�![]() ˳ʱ����ת
˳ʱ����ת![]() ��
��![]() ���õ�
���õ�![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() ��
��![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() ����
����![]() Ϊ����������ʱ����ֱ��д���߶�
Ϊ����������ʱ����ֱ��д���߶�![]() �ij���
�ij���

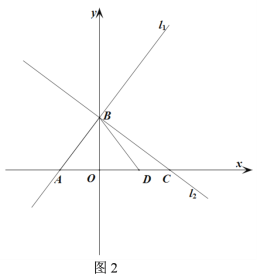
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�����У���ȷ���ǣ� ��
A.x2?x3=x6
B.![]() =|x|
=|x|
C.��x2�� ![]() ����x=x��1
����x=x��1
D.x2��x+1=��x�� ![]() ��2+
��2+ ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ֱˮƽ���������ߣ�ʱ��Ϊt���룩ʱ������������ĸ߶�h���ף����ù�ʽh=20t��5t2��0��t��4����
��1����t=3ʱ��������������ĸ߶ȣ�
��2��������������ĸ߶�Ϊ10��ʱ����t��
��3��������ʵ��t1 �� t2��t1��t2����t=t1��t2ʱ������������ĸ߶ȶ�Ϊm���ף�����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����������ABCD�У�E��F�ֱ��DZ�BC��CD�ϵĵ㣬�ҡ�EAF=45�����ѡ�ADF���ŵ�A˳ʱ����ת90���õ���ABG����ֱ��д��ͼ�����е�ȫ�������Σ�
��2�����ı���ABCD�У�AB=AD����B=��D=90��.
����ͼ2����E��F�ֱ��DZ�BC��CD�ϵĵ㣬��2��EAF=��BAD����֤��EF=BE+DF��
����E��F�ֱ��DZ�BC��CD�ӳ����ϵĵ㣬��2��EAF=��BAD�����еĽ����Ƿ���Ȼ��������˵������
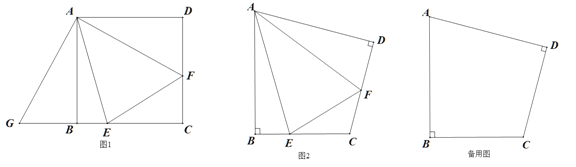
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
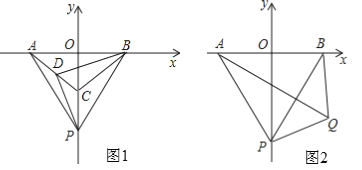
����Ŀ����֪����ͼ1����ƽ��ֱ������ϵ�У���A��B��C�����������ϣ���OA=OB=OC����ABC�����Ϊ9����P��C�������y�Ḻ������1����λ/����ٶ������˶�������PA��PB��D����m����m��ΪAC�ϵĵ㣨m��0��
��1���Էֱ����A��B��C��������ꣻ
��2�����P�˶���ʱ��Ϊt�룬�ʣ���tΪ��ֵʱ��DP��DB��ֱ����ȣ���˵�����ɣ�
��3����ͼ2����PA=AB���ڵ�����������һ����Q����QA��QB��QP���ҡ�PQA=60������Q�ڵ����������˶�ʱ�����APQ���PBQ�Ķ����ͣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com