
����Ŀ����֪����ͼ1����ƽ��ֱ������ϵ�У���A��B��C�����������ϣ���OA=OB=OC����ABC�����Ϊ9����P��C�������y�Ḻ������1����λ/����ٶ������˶�������PA��PB��D����m����m��ΪAC�ϵĵ㣨m��0��
��1���Էֱ����A��B��C��������ꣻ
��2�����P�˶���ʱ��Ϊt�룬�ʣ���tΪ��ֵʱ��DP��DB��ֱ����ȣ���˵�����ɣ�
��3����ͼ2����PA=AB���ڵ�����������һ����Q����QA��QB��QP���ҡ�PQA=60������Q�ڵ����������˶�ʱ�����APQ���PBQ�Ķ����ͣ�
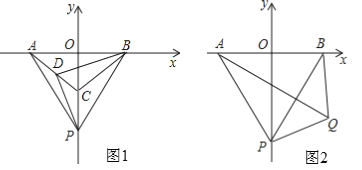
���𰸡���1��A����3��0����B��3��0����C��0����3������2����t=3��ʱ�� DP��DB��ֱ����ȣ����ɼ���������3����APQ+��PBQ=120�㣮
��������
��1������OA=OB=OC����AOC=��BOC=90�� �ó���ACB=90������������ABC�����Ϊ9���ó�OA=OC=OB=3 ���ɵó���������ꣻ
��2����DM��x���ڵ�M����DN��y���ڵ�N�������D������꣬�����ó���PCD�ա�BOD�������õ���BDP=��ODC=90������DP��DB��
��3����QA�Ͻ�ȡQS=QP������PS�����á�PQA=60�����ó���QSP�ǵȱ������Σ������ó���APS�ա�BPQ���Ӷ��ó���APQ+��PBQ=��APQ+��PAS�ó��𰸣�
��1��A����3��0����B��3��0����C��0����3����
��2����t=3��ʱ�� DP��DB��ֱ����ȣ�
�������£�����OD����DM��x���ڵ�M����DN��y���ڵ�N��
��D����m����m����
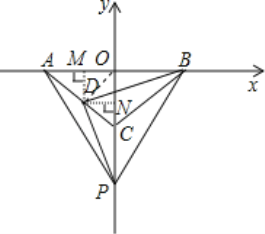
��DM=DN=OM=ON=m��
���DOM=��DON=45��������ACO=45�㣬
��DC=DO����ODC=90��
�ߡ�ODB+��BDC=��CDP+��BDC=90��
���ODB =��CDP
�� ��DP=DB
�� ��PCD�ա�BOD ��SAS��
��DP=DB����PDC=��BDO��
���BDP=��ODC=90�㣬
��DP��DB.
�� PC=BO
�� t=3 ��
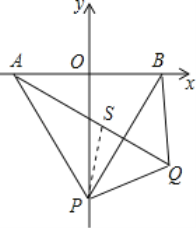
��3����QA�Ͻ�ȡQS=QP������PS��
�ߡ�PQA=60�㣬
���QSP�ǵȱ������Σ�
��PS=PQ����SPQ=60�㣬
��PO��AB�Ĵ�ֱƽ���ߣ�
��PA=PB ��PA=AB��
���PAB�ǵȱ������Σ�
���APB=60�㣬
���APS=��BPQ��
���APS�ա�BPQ��
���PAS=��PBQ��
���APQ+��PBQ=��APQ+��PAS=120�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����A=��C����P�ڱ�AB�ϣ� 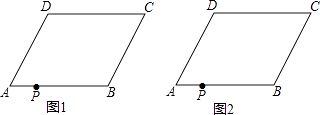
��1���ж��ı���ABCD����״������֤����
��2����AB=AD���Թ���P��ֱ��Ϊ�ᣬ���ı���ABCD�۵���ʹ��B��C�ֱ����ڵ�B�䡢C���ϣ���B��C�侭����D���ۺ����ı��ε���һ����ΪQ��
����ͼ2�������ı���PB��C��Q��������ͼ�ۼ�������˵�����������ɣ���
�������C=60�㣬��ô ![]() Ϊ��ֵʱ��B��P��AB��
Ϊ��ֵʱ��B��P��AB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�������ABCD�У�AD��BC��CAƽ�֡�BCD����B=60�㣬��AD=3��������ABCD���ܳ�Ϊ�� �� 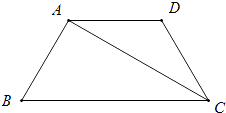
A.12 ![]()
B.15 ![]()
C.12
D.15
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ����1��0������3��0������ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��CD��
��1�����C��D�����꼰ƽ���ı���ABDC�����![]() .
.
��2����y�����Ƿ����һ��P������PA��PB��ʹ![]() ��2
��2![]() ������������һ�㣬�����P�����꣬�������ڣ���˵�����ɣ�
������������һ�㣬�����P�����꣬�������ڣ���˵�����ɣ�
��3����P���ı���ABCD���ϵĵ㣬����OPCΪ����������ʱ��ֱ��д����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����ϣ���ʦ�������ɸ���ͼ1������ֽƬ��A��ֽƬ�߳�Ϊa�������Σ�B��ֽƬ�DZ߳�Ϊb�������Σ�C��ֽƬ��Ϊa����Ϊb�ij����Σ�����A��ֽƬһ�ţ�B��ֽƬ�ţ�C��ֽƬ����ƴ����ͼ2�Ĵ������Σ�

��1���������ֲ�ͬ�ķ�����ͼ2�������ε������
����1���� ��������2���� ��
��2���۲�ͼ2������д��������������ʽ����a+b��2��a2+b2��ab֮��ĵ�����ϵ���� ��
��3�����ݣ�2�����еĵ�����ϵ������������⣺
����֪��a+b=5��a2+b2=11����ab��ֵ��
����֪��2018��a��2+��a��2017��2=5����2018��a����a��2017����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB=90����AB=2��BC=AC��DΪAB���е㣬EΪBC��һ�㣬����BDE��DE���ۣ��õ���FDE��EF��AC�ڵ�G�����ECG���ܳ���___________��
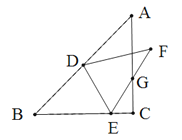
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABC�У�AB=AC����D��BC���е㣬��E��AD�ϣ�

��1����֤��BE=CE��
��2����ͼ2����BE���ӳ��߽�AC�ڵ�F����BF��AC������ΪF����BAC=45�㣬ԭ���������������䣮��֤����AEF�ա�BCF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ��ֱ��������ֽƬOAB��������AOB=90�㣬OA=2��OB=4����ͼ������ֽƬ������ƽ��ֱ������ϵ�У��۵���ֽƬ���ۺ����OB���ڵ�C�����AB���ڵ�D��
��1�����۵���ʹ��B���A�غϣ����C�����꣮
��2�����۵����B���ڱ�OA�ϵĵ�ΪB�����Ƿ���ڵ�B����ʹ���ı���BCB��D�����Σ������ڣ���˵�����ɲ�������εı߳����������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʵ��m��n�����ʽ![]() ����m��nǡ���ǵ�����ABC�������ߵı߳������ABC���ܳ���_______��
����m��nǡ���ǵ�����ABC�������ߵı߳������ABC���ܳ���_______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com