
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.

(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
【答案】(1)根据等腰三角形三线合一的性质可得∠BAE=∠EAC,然后利用“边角边”证明△ABE和△ACE全等,再根据全等三角形对应边相等证明即可。
(2)先判定△ABF为等腰直角三角形,再根据等腰直角三角形的两直角边相等可得AF=BF,再根据同角的余角相等求出∠EAF=∠CBF,然后利用“角边角”证明△AEF和△BCF全等即可。
【解析】
(1)根据等腰三角形三线合一的性质可得∠BAE=∠EAC,然后利用“边角边”证明△ABE和△ACE全等,再根据全等三角形对应边相等证明即可。
(2)先判定△ABF为等腰直角三角形,再根据等腰直角三角形的两直角边相等可得AF=BF,再根据同角的余角相等求出∠EAF=∠CBF,然后利用“角边角”证明△AEF和△BCF全等即可。
证明:(1)∵AB=AC,D是BC的中点,∴∠BAE=∠EAC。
在△ABE和△ACE中,∵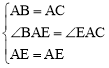 ,
,
∴△ABE≌△ACE(SAS)。∴BE=CE。
(2)∵∠BAC=45°,BF⊥AF,∴△ABF为等腰直角三角形。∴AF=BF。
∵AB=AC,点D是BC的中点,∴AD⊥BC。∴∠EAF+∠C=90°。
∵BF⊥AC,∴∠CBF+∠C=90°。∴∠EAF=∠CBF。
在△AEF和△BCF中,∵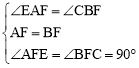 ,
,
∴△AEF≌△BCF(ASA)。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了解全市九年级学生某次数学模拟考试情况,现从全市30000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
分数段 | 频数 | 频率 |
x<60 | 20 | 0.10 |
60≤x<70 | 28 | 0.14 |
70≤x<80 | 54 | 0.27 |
80≤x<90 | a | 0.20 |
90≤x<100 | 24 | 0.12 |
100≤x<110 | 18 | b |
110≤x<120 | 16 | 0.08 |
请根据以上图表提供的信息,解答下列问题:
(1)表格中的a= ,b= ;
(2)请补全频数分布直方图;
(3)如果把成绩在90分以上(含90分)定为优秀,那么该市30000名九年级学生中本次数学模拟考试成绩为优秀的学生约有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,线段![]() cm,点C从点P出发以1cm/s的速度沿AB向左运动,点D从点B出发以2cm/s的速度沿AB向左运动(点C在线段AP上,D在线段BP上)
cm,点C从点P出发以1cm/s的速度沿AB向左运动,点D从点B出发以2cm/s的速度沿AB向左运动(点C在线段AP上,D在线段BP上)
(1)若C,D 运动到任意时刻都有PD=2AC,试说明PB=2AP;
(2)在(1)的条件下,Q是直线AB上一点,若AQ-BQ=PQ,求PQ的值;
(3)在(1)的条件下,若C,D运动了一段时间后恰有AB=2CD,这时点C停止运动,点D继续在线段PB上运动,M,N 分别是CD,PD的中点,求MN的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦晚会上,王老师要为她的学生及班级的六位科任老师送上贺年卡,网上购买贺年卡的优惠条件是:购买50或50张以上享受团购价.王老师发现:零售价与团购价的比是5:4,王老师计算了一下,按计划购买贺年卡只能享受零售价,如果比原计划多购买6张贺年卡就能享受团购价,这样她正好花了100元,而且比原计划还节约10元钱;
(1)贺年卡的零售价是多少?
(2)班里有多少学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(m,n),且满足m-2+(n-2)2=0,过A作AB⊥y轴,垂足为B.
(1)求A点坐标;
(2)如图1,分别以AB,AO为边作等边△ABC和△AOD,试判定线段AC和DC的数量关系和位置关系,并说明理由;
(3)如图2,过A作AE⊥x轴,垂足为E,点F、G分别为线段OE、AE上的两个动点 (不与端点重合),满足∠FBG=45°,设OF=a,AG=b,FG=c,试探究![]() 的值是 否为定值?如果是,直接写出此定值:如果不是,请举例说明.
的值是 否为定值?如果是,直接写出此定值:如果不是,请举例说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
【1】新知学习
⑴梯形的中位线:连接梯形两腰中点的线段叫做梯形的中位线.
⑵梯形的中位线性质:梯形的中位线平行于两底,并且等于两底和的一半.
⑶形如分式 ![]() (m为常数,且m>0),若x>0,则
(m为常数,且m>0),若x>0,则 ![]() ,并且有下列结论:
,并且有下列结论:
当x 逐渐增大时,分母x+2m逐渐增大,分式 ![]() 的值逐渐减少并趋于0,但仍大于0.当x 逐渐减少时,分母x+2m逐渐减少,分式
的值逐渐减少并趋于0,但仍大于0.当x 逐渐减少时,分母x+2m逐渐减少,分式 ![]() 的值逐渐增大并趋于
的值逐渐增大并趋于 ![]() ,即趋于
,即趋于 ![]() ,但仍小于
,但仍小于 ![]() .
.
【2】问题解决
如图2,已知在梯形ABCD中,AD∥BC,AD<BC,E、F分别是AB、CD的中点.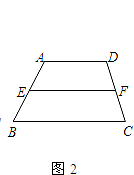
(1)设AD=7,BC=17,求 ![]() 的值.
的值.
(2)设AD=a(a为正的常数),BC=x,请问:当BC的长不断增大时, ![]() 的值能否大于或等于3,试证明你的结论.
的值能否大于或等于3,试证明你的结论.
(3)进一步猜想:任何一个梯形的中位线所分成的两部分图形的面积的比值所在的范围是什么,并说明理由.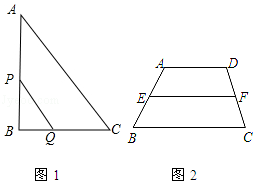
查看答案和解析>>
科目:初中数学 来源: 题型:
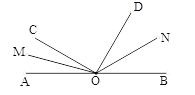
【题目】如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD 的平分线.
(1)知∠AOC=40°,∠BOD=60°,求∠MON的度数;
(2)知∠COD=90°,求出∠MON的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com