
ЁОЬтФПЁПЮЪЬтЬНОПЃК
ЁО1ЁПаТжЊбЇЯА
ЂХЬнаЮЕФжаЮЛЯпЃКСЌНгЬнаЮСНбќжаЕуЕФЯпЖЮНазіЬнаЮЕФжаЮЛЯпЃЎ
ЂЦЬнаЮЕФжаЮЛЯпаджЪЃКЬнаЮЕФжаЮЛЯпЦНаагкСНЕзЃЌВЂЧвЕШгкСНЕзКЭЕФвЛАыЃЎ
ЂЧаЮШчЗжЪН ![]() ЃЈmЮЊГЃЪ§ЃЌЧвmЃО0ЃЉЃЌШєxЃО0ЃЌдђ
ЃЈmЮЊГЃЪ§ЃЌЧвmЃО0ЃЉЃЌШєxЃО0ЃЌдђ ![]() ЃЌВЂЧвгаЯТСаНсТлЃК
ЃЌВЂЧвгаЯТСаНсТлЃК
ЕБx ж№НЅдіДѓЪБЃЌЗжФИx+2mж№НЅдіДѓЃЌЗжЪН ![]() ЕФжЕж№НЅМѕЩйВЂЧїгк0ЃЌЕЋШдДѓгк0ЃЎЕБx ж№НЅМѕЩйЪБЃЌЗжФИx+2mж№НЅМѕЩйЃЌЗжЪН
ЕФжЕж№НЅМѕЩйВЂЧїгк0ЃЌЕЋШдДѓгк0ЃЎЕБx ж№НЅМѕЩйЪБЃЌЗжФИx+2mж№НЅМѕЩйЃЌЗжЪН ![]() ЕФжЕж№НЅдіДѓВЂЧїгк
ЕФжЕж№НЅдіДѓВЂЧїгк ![]() ЃЌМДЧїгк
ЃЌМДЧїгк ![]() ЃЌЕЋШдаЁгк
ЃЌЕЋШдаЁгк ![]() ЃЎ
ЃЎ
ЁО2ЁПЮЪЬтНтОі
ШчЭМ2ЃЌвбжЊдкЬнаЮABCDжаЃЌADЁЮBCЃЌADЃМBCЃЌEЁЂFЗжБ№ЪЧABЁЂCDЕФжаЕуЃЎ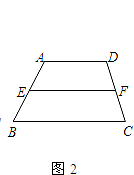
ЃЈ1ЃЉЩшAD=7ЃЌBC=17ЃЌЧѓ ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ2ЃЉЩшAD=aЃЈaЮЊе§ЕФГЃЪ§ЃЉЃЌBC=xЃЌЧыЮЪЃКЕБBCЕФГЄВЛЖЯдіДѓЪБЃЌ ![]() ЕФжЕФмЗёДѓгкЛђЕШгк3ЃЌЪджЄУїФуЕФНсТлЃЎ
ЕФжЕФмЗёДѓгкЛђЕШгк3ЃЌЪджЄУїФуЕФНсТлЃЎ
ЃЈ3ЃЉНјвЛВНВТЯыЃКШЮКЮвЛИіЬнаЮЕФжаЮЛЯпЫљЗжГЩЕФСНВПЗжЭМаЮЕФУцЛ§ЕФБШжЕЫљдкЕФЗЖЮЇЪЧЪВУДЃЌВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКЩшЬнаЮADFEЕФИпЮЊhЃЌдђЬнаЮBCFEЕФИпЮЊhЃЌ
ЁпEЁЂFЗжБ№ЪЧABЁЂCDЕФжаЕуЃЌ
ЁрEFЪЧЬнаЮABCDЕФжаЮЛЯпЃЌ
ЁрEFЁЮADЁЮBCЃЌEF= ![]() ЃЈAD+BCЃЉ=
ЃЈAD+BCЃЉ= ![]() ЃЈ7+17ЃЉ=12ЃЌ
ЃЈ7+17ЃЉ=12ЃЌ
Ёр ![]() =
= 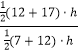 =
= ![]()
ЃЈ2ЃЉ
НтЃКЕБBCЕФГЄВЛЖЯдіДѓЪБЃЌ ![]() ЕФжЕВЛФмДѓгкЛђЕШгк3ЃЛРэгЩШчЯТЃК
ЕФжЕВЛФмДѓгкЛђЕШгк3ЃЛРэгЩШчЯТЃК
ЁпEЁЂFЗжБ№ЪЧABЁЂCDЕФжаЕуЃЌ
ЁрEFЪЧЬнаЮABCDЕФжаЮЛЯпЃЌ
ЁрEF= ![]() ЃЈAD+BCЃЉ=
ЃЈAD+BCЃЉ= ![]() ЃЈa+xЃЉЃЌ
ЃЈa+xЃЉЃЌ
гЩЃЈ1ЃЉЕУЃК ![]() =
=  =
= ![]() ЃЌ
ЃЌ
ЕБBCЕФГЄxВЛЖЯдіДѓЪБЃЌ ![]() ЕФЗжзгa+3xж№НЅдіДѓВЂЧїгкЃЌМДЧїгк3ЃЌЕЋШдаЁгк3ЃЛ
ЕФЗжзгa+3xж№НЅдіДѓВЂЧїгкЃЌМДЧїгк3ЃЌЕЋШдаЁгк3ЃЛ
ЁрЕБBCЕФГЄВЛЖЯдіДѓЪБЃЌ ![]() ЕФжЕВЛФмДѓгкЛђЕШгк3
ЕФжЕВЛФмДѓгкЛђЕШгк3
ЃЈ3ЃЉ
НтЃКШЮКЮвЛИіЬнаЮЕФжаЮЛЯпЫљЗжГЩЕФСНВПЗжЭМаЮЕФУцЛ§ЕФБШжЕЫљдкЕФЗЖЮЇЪЧДѓгк1ЖјаЁгк3ЃЛРэгЩШчЯТЃК
гЩЃЈ2ЃЉЕУЃК ![]() =
= ![]() ЃМ3ЃЌЕБx ж№НЅМѕЩйЪБЃЌЗжФИ3a+xж№НЅМѕЩйЃЌxЧїгкaЃЌ
ЃМ3ЃЌЕБx ж№НЅМѕЩйЪБЃЌЗжФИ3a+xж№НЅМѕЩйЃЌxЧїгкaЃЌ
дђa+3xЧїгк4aЃЌ3a+xЧїгк4aЃЌ
Ёр ![]() =
= ![]() ЕФжЕЧїгк1ЃЌЕЋДѓгк1ЃЌ
ЕФжЕЧїгк1ЃЌЕЋДѓгк1ЃЌ
Ёр1ЃМ ![]() ЃМ3ЃЌ
ЃМ3ЃЌ
ЙЪШЮКЮвЛИіЬнаЮЕФжаЮЛЯпЫљЗжГЩЕФСНВПЗжЭМаЮЕФУцЛ§ЕФБШжЕЫљдкЕФЗЖЮЇЪЧДѓгк1ЖјаЁгк3
ЁОНтЮіЁПЮЪЬтНтОіЃЈ1ЃЉЩшЬнаЮADFEЕФИпЮЊhЃЌдђЬнаЮBCFEЕФИпЮЊhЃЌжЄГіEFЪЧЬнаЮABCDЕФжаЮЛЯпЃЌгЩЬнаЮжаЮЛЯпЖЈРэЕУГіEFЁЮADЁЮBCЃЌEF= ![]() ЃЈAD+BCЃЉ=12ЃЌгЩЬнаЮУцЛ§ЙЋЪНМДПЩЕУГіД№АИЃЛЃЈ2ЃЉгЩЬнаЮжаЮЛЯпЖЈРэЕУГіEF=
ЃЈAD+BCЃЉ=12ЃЌгЩЬнаЮУцЛ§ЙЋЪНМДПЩЕУГіД№АИЃЛЃЈ2ЃЉгЩЬнаЮжаЮЛЯпЖЈРэЕУГіEF= ![]() ЃЈAD+BCЃЉ=
ЃЈAD+BCЃЉ= ![]() ЃЈa+xЃЉЃЌгЩЃЈ1ЃЉЕУЃК
ЃЈa+xЃЉЃЌгЩЃЈ1ЃЉЕУЃК ![]() =
=  =
= ![]() ЃЌЕБBCЕФГЄxВЛЖЯдіДѓЪБЃЌ
ЃЌЕБBCЕФГЄxВЛЖЯдіДѓЪБЃЌ ![]() ЕФЗжзгa+3xж№НЅдіДѓВЂЧїгкЃЌМДЧїгк3ЃЌЕЋШдаЁгк3ЃЛЃЈ3ЃЉгЩЃЈ2ЃЉЕУЃК
ЕФЗжзгa+3xж№НЅдіДѓВЂЧїгкЃЌМДЧїгк3ЃЌЕЋШдаЁгк3ЃЛЃЈ3ЃЉгЩЃЈ2ЃЉЕУЃК ![]() =
= ![]() ЃМ3ЃЌЕБx ж№НЅМѕЩйЪБЃЌЗжФИ3a+xж№НЅМѕЩйЃЌxЧїгкaЃЌдђa+3xЧїгк4aЃЌ3a+xЧїгк4aЃЌЕУГі
ЃМ3ЃЌЕБx ж№НЅМѕЩйЪБЃЌЗжФИ3a+xж№НЅМѕЩйЃЌxЧїгкaЃЌдђa+3xЧїгк4aЃЌ3a+xЧїгк4aЃЌЕУГі ![]() =
= ![]() ЕФжЕЧїгк1ЃЌЕЋДѓгк1ЃЌМДПЩЕУГіД№АИЃЎ
ЕФжЕЧїгк1ЃЌЕЋДѓгк1ЃЌМДПЩЕУГіД№АИЃЎ
ЁОПМЕуОЋЮіЁПИљОнЬтФПЕФвбжЊЬѕМўЃЌРћгУЬнаЮЕФжаЮЛЯпЕФЯрЙижЊЪЖПЩвдЕУЕНЮЪЬтЕФД№АИЃЌашвЊеЦЮеЬнаЮЕФжаЮЛЯпЦНаагкЬнаЮЕФСНЕзВЂЕШгкСНЕзКЭЕФвЛАыЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЪ§жсЩЯЕуAБэЪОЕФгаРэЪ§ЮЊЉ6ЃЌЕуBБэЪОЕФгаРэЪ§ЮЊ6ЃЌЕуPДгЕуAГіЗЂвдУПУы4ИіЕЅЮЛГЄЖШЕФЫйЖШдкЪ§жсЩЯгЩAЯђBдЫЖЏЃЌЕБЕуPЕНДяЕуBКѓСЂМДЗЕЛиЃЌШдШЛвдУПУы4ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏжСЕуAЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtЃЈЕЅЮЛЃКУыЃЉЃЎ
ЃЈ1ЃЉЧѓtЃН1ЪБЕуPБэЪОЕФгаРэЪ§ЃЛ
ЃЈ2ЃЉЧѓЕуPгыЕуBжиКЯЪБЕФtжЕЃЛ
ЃЈ3ЃЉдкЕуPбиЪ§жсгЩЕуAЕНЕуBдйЛиЕНЕуAЕФдЫЖЏЙ§ГЬжаЃЌЧѓЕуPгыЕуAЕФОрРыЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ4ЃЉЕБЕуPБэЪОЕФгаРэЪ§гыдЕуЕФОрРыЪЧ2ИіЕЅЮЛГЄЖШЪБЃЌЧыЧѓГіЫљгаТњзуЬѕМўЕФtжЕЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌAB=ACЃЌЕуDЪЧBCЕФжаЕуЃЌЕуEдкADЩЯЃЎ

ЃЈ1ЃЉЧѓжЄЃКBE=CEЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєBEЕФбгГЄЯпНЛACгкЕуFЃЌЧвBFЁЭACЃЌДЙзуЮЊFЃЌЁЯBAC=45ЁуЃЌдЬтЩшЦфЫќЬѕМўВЛБфЃЎЧѓжЄЃКЁїAEFЁеЁїBCFЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіЖрБпаЮЕФУПвЛИіФкНЧЖМЯрЕШЃЌВЂЧвУПИіЭтНЧЖМЕШгкКЭЫќЯрСкЕФФкНЧЕФвЛАыЃЎ
ЃЈ1ЃЉЧѓетИіЖрБпаЮЪЧМИБпаЮЃЛ
ЃЈ2ЃЉЧѓетИіЖрБпаЮЕФУПвЛИіФкНЧЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГШнЦїгЩAЁЂBЁЂCШ§ИіСЌЭЈГЄЗНЬхзщГЩЃЌЦфжаAЁЂBЁЂCЕФЕзУцЛ§ЗжБ№ЮЊ25cm2ЁЂ10cm2ЁЂ5cm2ЃЌCЕФШнЛ§ЪЧећИіШнЦїШнЛ§ЕФ![]() ЃЈШнЦїИїУцЕФКёЖШКіТдВЛМЦЃЉЃЌAЁЂBЕФзмИпЖШЮЊ12РхУзЃЎЯжвдОљдШЕФЫйЖШЃЈЕЅЮЛЃКcm3/minЃЉЯђШнЦїФкзЂЫЎЃЌжБЕНзЂТњЮЊжЙЃЎвбжЊЕЅЖРзЂТњAЁЂBЗжБ№ашвЊЕФЪБМфЮЊ10ЗжжгЁЂ8ЗжжгЃЎ
ЃЈШнЦїИїУцЕФКёЖШКіТдВЛМЦЃЉЃЌAЁЂBЕФзмИпЖШЮЊ12РхУзЃЎЯжвдОљдШЕФЫйЖШЃЈЕЅЮЛЃКcm3/minЃЉЯђШнЦїФкзЂЫЎЃЌжБЕНзЂТњЮЊжЙЃЎвбжЊЕЅЖРзЂТњAЁЂBЗжБ№ашвЊЕФЪБМфЮЊ10ЗжжгЁЂ8ЗжжгЃЎ
ЃЈ1ЃЉЧѓзЂТњећИіШнЦїЫљашЕФзмЪБМфЃЛ
ЃЈ2ЃЉЩшШнЦїAЕФИпЖШЮЊxcmЃЌдђШнЦїBЕФИпЖШЮЊЁЁ ЁЁcmЃЛ
ЃЈ3ЃЉЧѓШнЦїAЕФИпЖШКЭзЂЫЎЕФЫйЖШЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁЯAOB=30ЁуЃЌЁЯAOBФкгавЛЖЈЕуPЃЌЧвOP=12ЃЌдкOAЩЯгавЛЕуQЃЌOBЩЯгавЛЕуRЃЌШєЁїPQRжмГЄзюаЁЃЌдђзюаЁжмГЄЪЧ_____

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЖСЪщдТЛюЖЏжаЃЌФГаЃКХейШЋЬхЪІЩњЛ§МЋОшЪщЃЌЮЊСЫНтЫљОшЪщМЎЕФжжРрЃЌЭМЪщЙмРэдБЖдВПЗжЪщМЎНјааСЫГщбљЕїВщЃЌИљОнЕїВщЪ§ОнЛцжЦСЫШчЯТВЛЭъећЕФЭГМЦЭМБэЃЎЧыФуИљОнЭГМЦЭМБэЫљЬсЙЉЕФаХЯЂЛиД№ЯТУцЮЪЬтЃК ФГаЃЪІЩњОшЪщжжРрЧщПіЭГМЦБэ
жжРр | ЦЕЪ§ | АйЗжБШ |
AЃЎПЦЦеРр | 12 | 30% |
BЃЎЮФбЇРр | n | 35% |
CЃЎвеЪѕРр | m | 20% |
DЃЎЦфЫќРр | 6 | 15% |
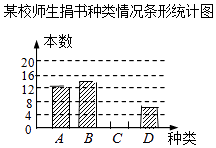
ЃЈ1ЃЉЭГМЦБэжаЕФn= ЃЌ ВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉБОДЮЛюЖЏЪІЩњЙВОшЪщ2000БОЃЌЧыЙРМЦгаЖрЩйБОПЦЦеРрЭМЪщЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌOMЪЧЁЯAOCЕФЦНЗжЯпЃЌONЪЧЁЯBOCЕФЦНЗжЯпЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЁЯAOBЪЧжБНЧЃЌЁЯBOC=60ЁуЪБЃЌЁЯMONЕФЖШЪ§ЪЧЖрЩйЃП
ЃЈ2ЃЉШчЭМ2ЃЌЕБЁЯAOB=ІСЃЌЁЯBOC=60ЁуЪБЃЌВТЯыЁЯMONгыІСЕФЪ§СПЙиЯЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕБЁЯAOB=ІСЃЌЁЯBOC=ІТЪБЃЌВТЯыЁЯMONгыІСЁЂІТгаЪ§СПЙиЯЕТ№ЃПШчЙћгаЃЌжИГіНсТлВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
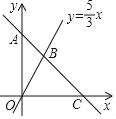
ЁОЬтФПЁПвЛДЮКЏЪ§y=kx+bЕФЭМЯѓОЙ§ЕуAЃЈ0ЃЌ9ЃЉЃЌВЂЧвгыжБЯпy=![]() xЯрНЛгкЕуBЃЌгыxжсЯрНЛгкЕуCЃЎ
xЯрНЛгкЕуBЃЌгыxжсЯрНЛгкЕуCЃЎ
ЃЈ1ЃЉШєЕуBЕФКсзјБъЮЊ3ЃЌЧѓBЕуЕФзјБъКЭkЃЌbЕФжЕЃЛ
ЃЈ2ЃЉдкyжсЩЯЪЧЗёДцдкетбљЕФЕуPЃЌЪЙЕУвдЕуPЃЌBЃЌAЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуPзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉдкжБЯпy=kx+bЩЯЪЧЗёДцдкЕуQЃЌЪЙЁїOBQЕФУцЛ§ЕШгк![]() ЃПШєДцдкЃЌЧыЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧыЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com