
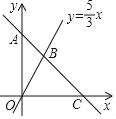
【题目】一次函数y=kx+b的图象经过点A(0,9),并且与直线y=![]() x相交于点B,与x轴相交于点C.
x相交于点B,与x轴相交于点C.
(1)若点B的横坐标为3,求B点的坐标和k,b的值;
(2)在y轴上是否存在这样的点P,使得以点P,B,A为顶点的三角形是等腰三角形?若存在,请直接写出点P坐标;若不存在,请说明理由.
(3)在直线y=kx+b上是否存在点Q,使△OBQ的面积等于![]() ?若存在,请求出点Q的坐标;若不存在,请说明理由.
?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)B(3,5),![]() ,b=9;(2)P1(0,9+
,b=9;(2)P1(0,9+![]() ),P2(0,9﹣
),P2(0,9﹣![]() ), P3(0,
), P3(0,![]() ),
),
P4(0,![]() );(3)Q(
);(3)Q(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)先根据函数y=![]() x求出B点坐标,再利用待定系数法求出k,b的值;
x求出B点坐标,再利用待定系数法求出k,b的值;
(2)先将两个函数组成方程组求得B点坐标,然后求出线段AB的长,再分别以A,B,P为顶点分类讨论得到P点的坐标;
(3)设Q点横坐标为a,根据点Q,C在直线![]() 上,得到Q,C的坐标,然后分情况讨论Q点的位置,再利用三角形面积公式求解得到a的值,从而得到Q点的坐标.
上,得到Q,C的坐标,然后分情况讨论Q点的位置,再利用三角形面积公式求解得到a的值,从而得到Q点的坐标.
解:(1)当x=3时,y=![]() x=
x=![]() ×3=5,即B(3,5),
×3=5,即B(3,5),
把A(0,9),B(3,5)代入y=kx+b得到![]() ,
,
解得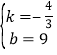 .
.
(2)由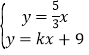 ,解得
,解得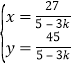 ,即B(
,即B(![]() ,
,![]() ),
),
∴AB=![]() .
.
①以A为顶点时,AB=AP,(1)P点在A点上方,P1(0,9+![]() ),
),
(2)P点在A点下方,P2(0,9﹣![]() );
);
②以B为顶点时,BA=BP,P3(0,![]() );
);
③以P为顶点时,PA=PB,P4(0,![]() ).
).
(3)设Q点的横坐标为a,
∵Q,C在直线![]() 上,
上,
∴Q(a,ka+9),C(﹣![]() ,0),
,0),
①当Q点在B点右侧时,
S△DBQ=![]() ×(﹣
×(﹣![]() )×(
)×(![]() ﹣ka﹣9)=
﹣ka﹣9)=![]() ,
,
∴a=![]() ,
,
代入函数![]() 解得:Q(
解得:Q(![]() ,
,![]() );
);
②当Q在点B左侧时,
S△BDQ=![]() ×(﹣
×(﹣![]() )×(ka+9﹣
)×(ka+9﹣![]() )=
)=![]() ,
,
∴a=![]() ,
,
代入函数![]() 解得:Q(
解得:Q(![]() ,
,![]() ),
),
综上所述,Q(![]() ,
,![]() )或
)或![]() ,
,![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
【题目】问题探究:
【1】新知学习
⑴梯形的中位线:连接梯形两腰中点的线段叫做梯形的中位线.
⑵梯形的中位线性质:梯形的中位线平行于两底,并且等于两底和的一半.
⑶形如分式 ![]() (m为常数,且m>0),若x>0,则
(m为常数,且m>0),若x>0,则 ![]() ,并且有下列结论:
,并且有下列结论:
当x 逐渐增大时,分母x+2m逐渐增大,分式 ![]() 的值逐渐减少并趋于0,但仍大于0.当x 逐渐减少时,分母x+2m逐渐减少,分式
的值逐渐减少并趋于0,但仍大于0.当x 逐渐减少时,分母x+2m逐渐减少,分式 ![]() 的值逐渐增大并趋于
的值逐渐增大并趋于 ![]() ,即趋于
,即趋于 ![]() ,但仍小于
,但仍小于 ![]() .
.
【2】问题解决
如图2,已知在梯形ABCD中,AD∥BC,AD<BC,E、F分别是AB、CD的中点.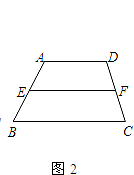
(1)设AD=7,BC=17,求 ![]() 的值.
的值.
(2)设AD=a(a为正的常数),BC=x,请问:当BC的长不断增大时, ![]() 的值能否大于或等于3,试证明你的结论.
的值能否大于或等于3,试证明你的结论.
(3)进一步猜想:任何一个梯形的中位线所分成的两部分图形的面积的比值所在的范围是什么,并说明理由.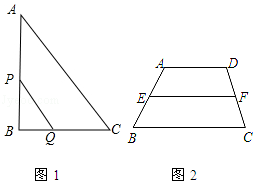
查看答案和解析>>
科目:初中数学 来源: 题型:
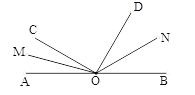
【题目】如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD 的平分线.
(1)知∠AOC=40°,∠BOD=60°,求∠MON的度数;
(2)知∠COD=90°,求出∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为海里(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4).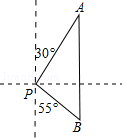
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(1,1),B(4,3),将点A向左平移2个单位长度,再向上平移3个单位长度得到点C.
(1)写出点C的坐标;
(2)画出△ABC并判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12cm2,则S△DGF的值为( )
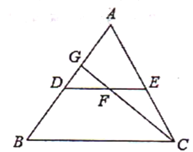
A.4cm2 B.6cm2 C.8cm2 D.9cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF. 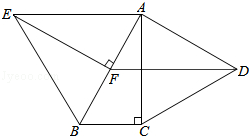
(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地走去,y1,y2分别表示小东、小明离B地的距离y(km)与所用时间x(h)的关系,如图所示,根据图象提供的信息,回答下列问题:

(1)试用文字说明交点P所表示的实际意义;
(2)求y1与x的函数关系式;
(3)求A,B两地之间的距离及小明到达A地所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是![]()
![]()
A. 有两个角和一条边对应相等的两个三角形全等
B. 有一条边和一个锐角对应相等的两个直角三角形全等
C. 有两边和其中一边的对角对应相等的两个三角形全等
D. 有两条直角边对应相等的两个直角三角形全等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com