
【题目】如图,已知一次函数y1=﹣x+a与x轴、y轴分别交于点D、C两点和反比例函数![]() 交于A、B两点,且点A的坐标是(1,3),点B的坐标是(3,m)
交于A、B两点,且点A的坐标是(1,3),点B的坐标是(3,m)
(1)求a,k,m的值;
(2)求C、D两点的坐标,并求△AOB的面积.
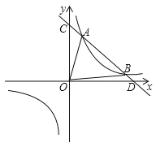
【答案】(1)4,3,1;(2)(0,4),(1,3),4
【解析】
(1)由于已知一次函数y1=-x+a和反比例函数![]() 交于A、B两点,且点A的坐标是(1,3),把A的坐标代入反比例函数解析式中即可确定k的值,然后利用解析式即可确定点B的坐标,最后利用A或B坐标即可确定a的值;
交于A、B两点,且点A的坐标是(1,3),把A的坐标代入反比例函数解析式中即可确定k的值,然后利用解析式即可确定点B的坐标,最后利用A或B坐标即可确定a的值;
(2)利用(1)中求出的直线的解析式可以确定C,D的坐标,然后利用面积的割补法可以求出△AOB的面积.
解:(1)∵反比例函数![]() 经过A、B两点,且点A的坐标是(1,3),
经过A、B两点,且点A的坐标是(1,3),
∴3=![]() ,
,
∴k=3,
而点B的坐标是(3,m),∴m=![]() =1,
=1,
∵一次函数y1=﹣x+a经过A点,且点A的坐标是(1,3),
∴3=﹣1+a,
∴a=4.
(2)∵y1=﹣x+4,当x=0时,y=4,当y=0时,x=4,
∴C的坐标为(0,4),D的坐标为(4,0),
∴S△AOB=S△COB﹣S△COA=![]() ×4×3﹣
×4×3﹣![]() ×4×1=4.
×4×1=4.


科目:初中数学 来源: 题型:
【题目】学校为奖励在家自主学习有突出表现的学生,决定购买笔记本和钢笔作为奖品.已知1本笔记本和4支钢笔共需100元,4本笔记本和6支钢笔共需190元.
(1)分别求一本笔记本和一支钢笔的售价;
(2)若学校准备购进这两种奖品共90份,并且笔记本的数量不多于钢笔数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
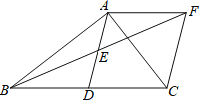
【题目】如图,在![]() ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:![]() AEF≌△DEB;
AEF≌△DEB;
(2)若∠BAC=90°,求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.
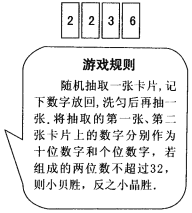
(1)求随机抽取一张卡片,恰好得到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树形图法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织师生共60人,从甲地乘动车前往乙地参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
甲地 | 乙地 | 26 | 22 | 16 |
若师生均购买二等座票,则共需1020元.
(1)求参加活动的教师和学生各有多少人?
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,后续前往的教师和学生均购买二等座票.设提早前往的教师有![]() 人,购买一、二等座票全部费用为
人,购买一、二等座票全部费用为![]() 元.
元.
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若购买一、二等座票全部费用不多于1030元,则提早前往的教师最多只能有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户要改造部分农田种植蔬菜.经调查,平均每亩改造费用是900元,添加辅助设备费用(元)与改造面积(亩)的平方成正比,比例系数为18,以上两项费用三年内不需再投入;每亩种植蔬菜还需种子、人工费用600元,这项费用每年均需再投入,除上述费用外,没有其他费用,设改造![]() 亩,每亩蔬菜年销售额为
亩,每亩蔬菜年销售额为![]() 元.
元.
(1)设改造当年收益为![]() 元,用含
元,用含![]() ,
,![]() 的式子表示
的式子表示![]() ;
;
(2)按前三年计算,若![]() ,是否改造面积越大收益越大?改造面积为多少时,可以得到最大收益?
,是否改造面积越大收益越大?改造面积为多少时,可以得到最大收益?
(3)若![]() ,按前三年计算,能确保改造的面积越大收益也越大,求
,按前三年计算,能确保改造的面积越大收益也越大,求![]() 的取值范围.
的取值范围.
注:收益=销售额-(改造费+辅助设备费+种子、人工费).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:A:![]() ;B:
;B:![]() ;C:
;C:![]() ;D:
;D:![]() ,并绘制出如下不完整的统计图.
,并绘制出如下不完整的统计图.

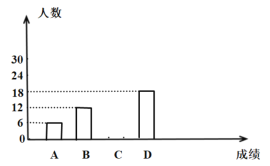
(1)求被抽取的学生成绩在C:![]() 组的有多少人;
组的有多少人;
(2)所抽取学生成绩的中位数落在哪个组内;
(3)若该学校有![]() 名学生,估计这次竞赛成绩在A:
名学生,估计这次竞赛成绩在A:![]() 组的学生有多少人.
组的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李莉在五张完全相同并且没有任何标记的卡片的一面分别写下数据﹣4,﹣1,0,3,5,将写有数据的一面朝下放置,并混合均匀.
(1)随机摸起一张,求上面的数据为负数的概率;
(2)随机摸起两张,其中一张表示x,另一张表示y,求点(x,y)在直线y=﹣x﹣1上的概率;
(3)随机摸起一张,记为x,然后放回,混合均匀后再随机摸起一张,记为y,求点(x,y)是第四象限内的点的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com