
【题目】如图,直线![]() 分别与x轴,y轴交于点A,B两点,点C为OB的中点,抛物线
分别与x轴,y轴交于点A,B两点,点C为OB的中点,抛物线![]() 经过A,C两点.
经过A,C两点.

(1)求抛物线的函数表达式;
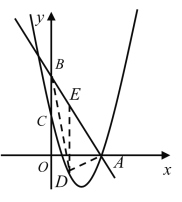
(2)点D是直线AB下方的抛物线上的一点,且![]() 的面积为
的面积为![]() ,求点D的坐标;
,求点D的坐标;
(3)点P为抛物线上一点,若![]() 是以AB为直角边的直角三角形,求点P到抛物线的对称轴的距离.
是以AB为直角边的直角三角形,求点P到抛物线的对称轴的距离.
【答案】(1)![]() ;(2)(2,-3);(3)
;(2)(2,-3);(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)由直线解析式求出A、B坐标,然后得出C点坐标,再用待定系数法求出抛物线解析式;
(2)过点D作DE⊥x轴,交直线AB于点E,设D(m,![]() ),利用S△ABD=
),利用S△ABD=![]() =
=![]() 得出方程,解出m值即可;
得出方程,解出m值即可;
(3)分点A是直角顶点和点B是直角顶点,结合图像,表示出△ABP三边长度,利用勾股定理得出方程,求解即可.
解:(1)直线![]() 中,
中,
令x=0,则y=10,令y=0,则x=5,
∴A(5,0),B(0,10),
∵点C是OB中点,
∴C(0,5),将A和C代入抛物线![]() 中,
中,
![]() ,解得:
,解得:![]() ,
,
∴抛物线表达式为:![]() ;
;
(2)联立:![]() ,
,
解得:![]() 或
或![]() ,
,
∴直线AB与抛物线交于点(-1,12)和(5,0),
∵点D是直线AB下方抛物线上的一点, 设D(m,![]() ),
),
∴-1<m<5,
过点D作DE⊥x轴,交直线AB于点E,
∴E(m,-2m+10),
∴DE=![]() =
=![]() ,
,
∴S△ABD=![]() =
=![]() =
=![]() ,
,
解得:m=2,
∴点D的坐标为(2,-3);
(3)抛物线表达式为:![]() ,
,
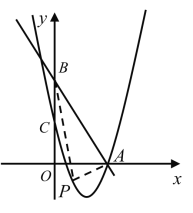
∵△APB是以AB为直角边的直角三角形,
设点P(n,![]() ),∵A(5,0),B(0,10),
),∵A(5,0),B(0,10),
∴AP2=![]() ,BP2=
,BP2=![]() ,AB2=125,
,AB2=125,
当点A为直角顶点时,
BP2= AB2+ AP2,
解得:n=![]() 或5(舍),
或5(舍),
当点B为直角顶点时,
AP2= AB2+ BP2,
解得:n=![]() 或
或![]() ,
,
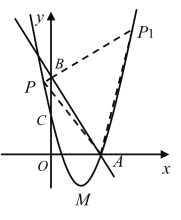
而抛物线对称轴为直线x=3,
则3-![]() =
=![]() ,
,![]() -3=
-3=![]() ,3-
,3-![]() =
=![]() ,
,
综上:点P到抛物线对称轴的距离为:![]() 或
或![]() 或
或![]() .
.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车沿同一公路从A地出发前往路程为100千米的B地,乙车比甲车晚出发15分钟,行驶过程中所行驶的路程分别用y1、y2(千米)表示,它们与甲车行驶的时间x(分钟)之间的函数关系如图所示.
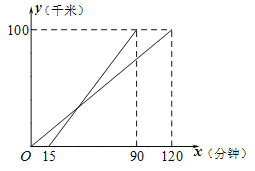
(1)分别求出y1、y2关于x的函数解析式并写出定义域;
(2)乙车行驶多长时间追上甲车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广元市某中学举行了“禁毒知识竞赛”,王老师将九年级(1)班学生成绩划分为A、B、C、D、E五个等级,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
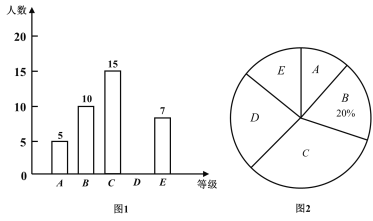
(1)求九年级(1)班共有多少名同学?
(2)补全条形统计图,并计算扇形统计图中的“C”所对应的圆心角度数;
(3)成绩为A类的5名同学中,有2名男生和3名女生;王老师想从这5名同学中任选2名同学进行交流,请用列表法或画树状图的方法求选取的2名同学都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
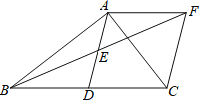
【题目】如图,在![]() ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:![]() AEF≌△DEB;
AEF≌△DEB;
(2)若∠BAC=90°,求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.
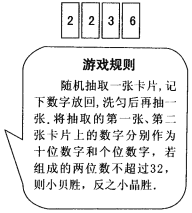
(1)求随机抽取一张卡片,恰好得到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树形图法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户要改造部分农田种植蔬菜.经调查,平均每亩改造费用是900元,添加辅助设备费用(元)与改造面积(亩)的平方成正比,比例系数为18,以上两项费用三年内不需再投入;每亩种植蔬菜还需种子、人工费用600元,这项费用每年均需再投入,除上述费用外,没有其他费用,设改造![]() 亩,每亩蔬菜年销售额为
亩,每亩蔬菜年销售额为![]() 元.
元.
(1)设改造当年收益为![]() 元,用含
元,用含![]() ,
,![]() 的式子表示
的式子表示![]() ;
;
(2)按前三年计算,若![]() ,是否改造面积越大收益越大?改造面积为多少时,可以得到最大收益?
,是否改造面积越大收益越大?改造面积为多少时,可以得到最大收益?
(3)若![]() ,按前三年计算,能确保改造的面积越大收益也越大,求
,按前三年计算,能确保改造的面积越大收益也越大,求![]() 的取值范围.
的取值范围.
注:收益=销售额-(改造费+辅助设备费+种子、人工费).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,水平桌面上有甲、乙、丙三个圆柱形容器,它们的高都为![]() 且甲、丙容器的底面积相同,乙容器在距离底部
且甲、丙容器的底面积相同,乙容器在距离底部![]() 高度处与甲、丙容器连通(联通处的体积忽略不计).甲容器中有水,水位高为
高度处与甲、丙容器连通(联通处的体积忽略不计).甲容器中有水,水位高为![]() .若用水管向乙容器中匀速注水,直至三个容器都注满水,乙容器中的水位
.若用水管向乙容器中匀速注水,直至三个容器都注满水,乙容器中的水位![]() 与注水时间
与注水时间![]() 之间的函数图象如图②所示.
之间的函数图象如图②所示.
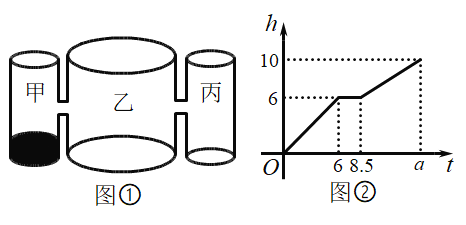
(1)甲、乙两容器的底面积之比为 ;
(2)图②中![]() 的值为 ;
的值为 ;
(3)若将注水管改为向容器丙中匀速注水,且注水速度不变,请在图③中画出容器丙中水位![]() 与注水时间
与注水时间![]() 之间的函数图象.
之间的函数图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com