
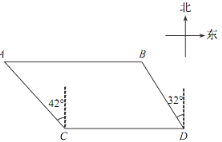
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的木栈道 AB ,栈道 AB 与景区道路CD 平行.在 C 处测得栈道一端 A 位于北偏西 42°方向,在 D 处测得栈道另一端 B 位于北偏西 32°方向.已知 CD =120 m , BD =80 m ,求木栈道 AB 的长度(结果保留整数) .
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】![]()
【解析】
过C作CE⊥AB于E,DF⊥AB交AB的延长线于F,于是得到CE∥DF,推出四边形CDFE是矩形,得到EF=CD=120,DF=CE,解直角三角形即可得到结论.
过C作CE⊥AB于E,DF⊥AB交AB的延长线于F,
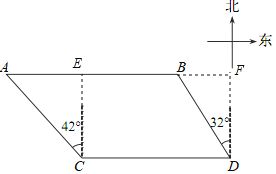
则CE∥DF,
∵AB∥CD,
∴四边形CDFE是矩形,
∴EF=CD=120,DF=CE,
在Rt△BDF中,∵∠BDF=32°,BD=80,
∴DF=cos32°BD=80×![]() ≈68,BF=sin32°BD=80×
≈68,BF=sin32°BD=80×![]() ,
,
∴BE=EF-BF=![]() ,
,
在Rt△ACE中,∵∠ACE=42°,CE=DF=68,
∴AE=CEtan42°=68×![]() ,
,
∴AB=AE+BE=![]() +
+![]() ≈139m,
≈139m,
答:木栈道AB的长度约为139m.


科目:初中数学 来源: 题型:
【题目】某校准备组织师生共60人,从甲地乘动车前往乙地参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
甲地 | 乙地 | 26 | 22 | 16 |
若师生均购买二等座票,则共需1020元.
(1)求参加活动的教师和学生各有多少人?
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,后续前往的教师和学生均购买二等座票.设提早前往的教师有![]() 人,购买一、二等座票全部费用为
人,购买一、二等座票全部费用为![]() 元.
元.
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若购买一、二等座票全部费用不多于1030元,则提早前往的教师最多只能有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图所示的一次函数关系.随着补贴数额的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足![]()
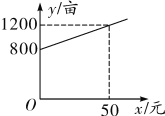
(1)求出政府补贴政策实施后,种植亩数y与政府补贴数额x之间的函数关系式;
(2)在政府出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?求出总收益w的最大值;
(4)该市希望这种蔬菜的总收益不低于7200000元,请你帮助该市确定每亩补贴数额的范围,在此条件下要使总收益最大,并说明每亩补贴数额应定为多少元合适?
参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是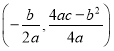 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂将![]() 四种型号的空调销售额的情况绘制成了图①和图②两幅尚不完整的统计图.
四种型号的空调销售额的情况绘制成了图①和图②两幅尚不完整的统计图.
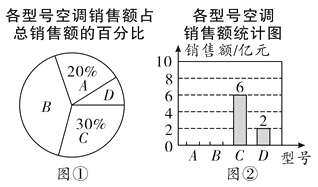
(1)请补全图②的条形统计图;
(2)为了应对激烈的市场竞争,该厂决定降价促销,![]() 四种型号的空调分别降价
四种型号的空调分别降价![]() ,因此该厂宣称其产品平均降价
,因此该厂宣称其产品平均降价![]() ,你认为该厂的说法正确吗?请通过计算说明理由;
,你认为该厂的说法正确吗?请通过计算说明理由;
(3)为进一步促销,该厂决定从这四种型号的空调中任意选取两种型号的空调降价销售,请用树状图或列表法求出降价空调中含D型号空调的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李莉在五张完全相同并且没有任何标记的卡片的一面分别写下数据﹣4,﹣1,0,3,5,将写有数据的一面朝下放置,并混合均匀.
(1)随机摸起一张,求上面的数据为负数的概率;
(2)随机摸起两张,其中一张表示x,另一张表示y,求点(x,y)在直线y=﹣x﹣1上的概率;
(3)随机摸起一张,记为x,然后放回,混合均匀后再随机摸起一张,记为y,求点(x,y)是第四象限内的点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交![]() 于点D,以OC为半径的
于点D,以OC为半径的![]() 交OA于点E,则图中阴影部分的面积是( )
交OA于点E,则图中阴影部分的面积是( )

A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC,∠ABC=90°,顶点A在第一象限,B、C在x轴的正半轴上(C在B的右侧),BC=3,AB=4,若双曲线![]() 交边AB于点E,交边AC于中点D.
交边AB于点E,交边AC于中点D.
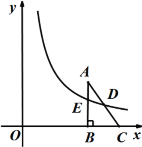
(1)若OB=2,求k;
(2)若AE=![]() , 求直线AC的解析式.
, 求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
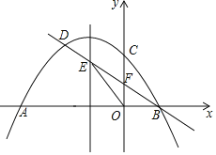
【题目】如图,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点B的直线与抛物线的另一个交点为D,与抛物线的对称轴交于点E,与y轴交于点F,且
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点B的直线与抛物线的另一个交点为D,与抛物线的对称轴交于点E,与y轴交于点F,且![]() ,△OBE的面积为
,△OBE的面积为![]() .
.
(1)求抛物线的解析式;
(2)设P为已知抛物线上的任意一点,当△ACP的面积等于△ACB的面积时,求点P的坐标;
(3)点Q(0,m)是y轴上的动点,连接AQ、BQ,当∠AQB为钝角时,则m的取值范围是 .(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com