
已知抛物线y=k(x+1)(x- )与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )
)与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )
A.2 B.3 C.4 D.5
C 解析:令y=0,则k(x+1)(x- )=0,解得x1=-1,x2=
)=0,解得x1=-1,x2= ,设A点坐标 为(-1,0),则B点的坐标为(
,设A点坐标 为(-1,0),则B点的坐标为( ,0).
,0).
当x=0时,y=-3,∴C(0,-3),AC=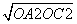 =
=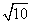 .
.
(1)k>0时,有以下3种情况:①当AC=BC时,点A、B分别在x轴的负半轴和正半轴上,且AO=BO,即1= ,解得k=3;②当AB=BC时,AB2=B
,解得k=3;②当AB=BC时,AB2=B C2=BO2+CO2,即(
C2=BO2+CO2,即( +1)2=(
+1)2=( )2+32,
)2+32, 解得k=
解得k=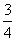 ;③当AB=AC时,AB2=AC2,即(
;③当AB=AC时,AB2=AC2,即( +1)2=10,解得k=
+1)2=10,解得k=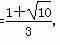 (k>0,舍去k=
(k>0,舍去k=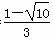 ).
).
(2)k<0时,点B只能在点A的左侧.只有当AB=AC时,△ABC可构成等腰三角形,∴- -1=
-1=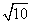 ,解得k=
,解得k=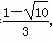 ,综上可知,当k1=3,k2=
,综上可知,当k1=3,k2=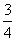 ,k3=
,k3=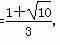 ,k4=
,k4=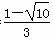 时,△ABC为等腰三角形,故能使△ABC为等腰三角形的抛物线的条数是4.
时,△ABC为等腰三角形,故能使△ABC为等腰三角形的抛物线的条数是4.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
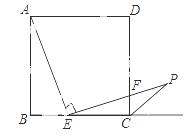
如图,在正方形ABCD中, 点E是BC边上的点,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,
点E是BC边上的点,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,
(1)求证:AE=EP;
(2)在AB边上是否存在点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
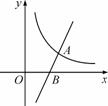
如图,直线y =2x-6与反比例函数y=
=2x-6与反比例函数y= (x>0)的图象交于点A(4,2),与x轴交于点B.
(x>0)的图象交于点A(4,2),与x轴交于点B.
(1)求k的值及B的坐标;
(2)在x轴上是 否存在点C,使得
否存在点C,使得 AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.
AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,反比例函数与 二次函数y=k(x2+x-1)的图象交于点A(1,k)和点B(-1,k).
二次函数y=k(x2+x-1)的图象交于点A(1,k)和点B(-1,k).
(1)当k=-2时,求反比例函数的解析式;
(2)要使反比例函数与二次函数都是y随着 x的增大而增大,求k应满足的条件以及x的取值范围.
x的增大而增大,求k应满足的条件以及x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
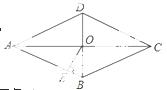
如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为( )
A.75° B.65° C.55° D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
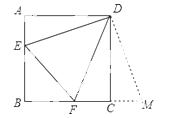
正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°。将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM (2)当AE=1时,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com