
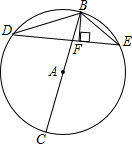
 如图,BC是⊙A的直径,△DBE的各个顶点在⊙A上,BF⊥DE于点F.求证:BD•BE=BC•BF.
如图,BC是⊙A的直径,△DBE的各个顶点在⊙A上,BF⊥DE于点F.求证:BD•BE=BC•BF. 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
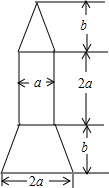 2013年6月11日17时18分,神舟十号载人飞船顺利升空,同学们倍受鼓舞,开展了火箭模型的制作比赛,如图为火箭模型的截面图:下面为等腰梯形,中间是长方形,上面是三角形.
2013年6月11日17时18分,神舟十号载人飞船顺利升空,同学们倍受鼓舞,开展了火箭模型的制作比赛,如图为火箭模型的截面图:下面为等腰梯形,中间是长方形,上面是三角形.查看答案和解析>>
科目:初中数学 来源: 题型:
 根据图填空
根据图填空查看答案和解析>>
科目:初中数学 来源: 题型:
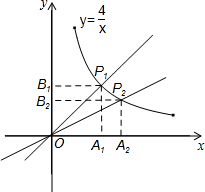 已知:如图,函数y=
已知:如图,函数y=| 4 |
| x |
| 1 |
| 2 |
| 1 |
| k |
查看答案和解析>>
科目:初中数学 来源: 题型:
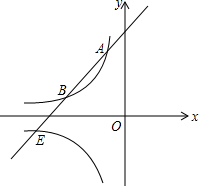 如图,已知直线y=ax+b过A(-1,6)与双曲线y=
如图,已知直线y=ax+b过A(-1,6)与双曲线y=| m |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| x | … | 8 | 9 | 10 | 11 | … |
| y | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com