
【题目】某商店销售一种成本为![]() 元
元![]() 的水产品,若按
的水产品,若按![]() 元
元![]() 销售,一个月可售出
销售,一个月可售出![]() ,售价毎涨
,售价毎涨![]() 元,月销售量就减少
元,月销售量就减少![]() .
.
![]() 写出月销售利润
写出月销售利润![]() (元)与售价
(元)与售价![]() (元
(元![]() )之间的函数表达式;
)之间的函数表达式;
![]() 当售价定为多少元时,该商店月销售利润为
当售价定为多少元时,该商店月销售利润为![]() 元?
元?
![]() 当售价定为多少元时会获得最大利润?求出最大利润.
当售价定为多少元时会获得最大利润?求出最大利润.
【答案】(1)y![]() ;(2)当售价定为
;(2)当售价定为![]() 元或
元或![]() 元时,该商店月销售利润为
元时,该商店月销售利润为![]() 元;
元;![]()
当售价为![]() 元,利润最大,最大利润是
元,利润最大,最大利润是![]() 元.
元.
【解析】
(1)根据月销售利润=每千克的利润×数量就可以表示出月销售利润y(单位:元)与售价x(单位:元/千克)之间的函数解析式;
(2)当y=8000时,代入(1)的解析式求出结论即可,
(3)将(1)的解析式化为顶点式就可以求出结论.
解:(1)由题意,得
y=(x-40)[500-10(x-50)],
y=-10x2+1400x-40000=![]() .
.
答:y与x之间的函数关系式为:y=-10x2+1400x-40000;
(2)由题意,得
8000=-10x2+1400x-40000,
解得:x1=60,x2=80.
答:销售单价应定为80元;
(3)∵y=-10x2+1400x-40000.
∴y=-10(x-70)2+9000.
∴a=-10<0,y有最大值.
∴当x=70时.y最大=9000元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里有1个红球,1个黄球和n个白球,它们除颜色外其余都相同.
(1)从这个袋子里摸出一个球,记录其颜色,然后放回,摇均匀后,重复该实验,经过大量实验后,发现摸到白球的频率稳定于0.5左右,求n的值;
(2)在(1)的条件下,先从这个袋中摸出一个球,记录其颜色,放回,摇均匀后,再从袋中摸出一个球,记录其颜色.请用画树状图或者列表的方法,求出先后两次摸出不同颜色的两个球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n是实数,定义运算“*”为:m*n=mn+n.
(1)分别求4*(﹣2)与4*![]() 的值;
的值;
(2)若关于x的方程x*(a*x)=﹣![]() 有两个相等的实数根,求实数a的值.
有两个相等的实数根,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( )
A.OA =OB =OC=OD,AC⊥BDB.AB∥CD,AC=BD
C.AD∥BC,∠A=∠CD.OA=OC,OB=OD,AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.
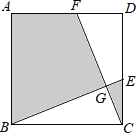
(1)求![]() BGC的度数;
BGC的度数;
(2)若CE=1,H为BF的中点时,求HG的长度;
(3)若图中阴影部分的面积与正方形ABCD的面积之比为2:3,求△BCG的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中CE⊥AB于E,BF⊥AC于F.
(1)求证:△AFB∽△AEC;
(2)求证:△AEFA∽△ABC;
(3)若∠A=60°时,求△AFE与△ABC面积之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,M为直线l:x=a上一点,N是直线l外一点,且直线MN与x轴不平行,若MN为某个矩形的对角线,且该矩形的边均与某条坐标轴垂直,则称该矩形为直线l的“伴随矩形”.如图为直线l的“伴随矩形”的示意图.

(1)已知点A在直线l:x=2上,点B的坐标为(3,﹣2)
①若点A的纵坐标为0,则以AB为对角线的直线l的“伴随矩形”的面积是 ;
②若以AB为对角线的直线l的“伴随矩形”是正方形,求直线AB的表达;
(2)点P在直线l:x=m上,且点P的纵坐标为4,若在以点(2,1),(﹣2,1),(﹣2,﹣1),(2,﹣1)为顶点的四边形上存在一点Q,使得以PQ为对角线的直线l的“伴随矩形”为正方形,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
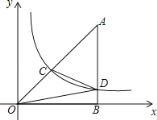
【题目】如图,△OAB中,∠ABO=90°,点A位于第一象限,点O为坐标原点,点B在x轴正半轴上,若双曲线y=![]() (x>0)与△OAB的边AO、AB分别交于点C、D,点C为AO的中点,连接OD、CD.若S△OBD=3,则S△OCD为( )
(x>0)与△OAB的边AO、AB分别交于点C、D,点C为AO的中点,连接OD、CD.若S△OBD=3,则S△OCD为( )
A.3B.4C.![]() D.6
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com