
【题目】已知m,n是实数,定义运算“*”为:m*n=mn+n.
(1)分别求4*(﹣2)与4*![]() 的值;
的值;
(2)若关于x的方程x*(a*x)=﹣![]() 有两个相等的实数根,求实数a的值.
有两个相等的实数根,求实数a的值.
【答案】(1)![]() ;(2)a=0.
;(2)a=0.
【解析】
(1)利用新定义得到4*(﹣2)=4×(﹣2)+(﹣2);4*![]() =4×
=4×![]() +
+![]() ,然后进行实数运算即可;
,然后进行实数运算即可;
(2)利用新定义得到x(ax+x)+ax+x=﹣![]() ,整理得(a+1)x2+(a+1)x+
,整理得(a+1)x2+(a+1)x+![]() =0,根据一元二次方程的定义和判别式的意义得到a+1≠0且△=(a+1)2﹣4(a+1)×
=0,根据一元二次方程的定义和判别式的意义得到a+1≠0且△=(a+1)2﹣4(a+1)×![]() =0,然后解关于a的方程即可.
=0,然后解关于a的方程即可.
(1)4*(﹣2)=4×(﹣2)+(﹣2)=﹣8﹣2=﹣10;
4*![]() =4×
=4×![]() +
+![]() =5
=5![]() ;
;
(2)a*x=ax+x,
由x*(ax+x)=﹣![]() 得x(ax+x)+ax+x=﹣
得x(ax+x)+ax+x=﹣![]() ,
,
整理得(a+1)x2+(a+1)x+![]() =0,
=0,
因为关于x的方程(a+1)x2+(a+1)x+![]() =0有两个相等的实数根,
=0有两个相等的实数根,
所以a+1≠0且△=(a+1)2﹣4(a+1)×![]() =0,
=0,
所以a=0.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,将函数![]() 的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )
的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
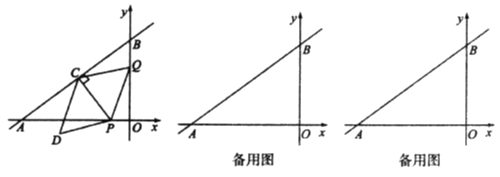
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴负方向以每秒1个单位长度的速度运动,同时动点
轴负方向以每秒1个单位长度的速度运动,同时动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向以每秒2个单位长度的速度运动,过点
方向以每秒2个单位长度的速度运动,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,以
,以![]() 、
、![]() 为邻边构造平行四边形
为邻边构造平行四边形![]() ,设点
,设点![]() 运动的时间为
运动的时间为![]() s.
s.
(1)当点![]() 在线段
在线段![]() 上时,用含
上时,用含![]() 的代数式表示
的代数式表示![]() 、
、![]() 的长.
的长.
(2)在运动过程中,①当点![]() 落在
落在![]() 轴上时,求出满足条件的
轴上时,求出满足条件的![]() 的值;②当点
的值;②当点![]() 落在
落在![]() 内部(不包括边界)时,直接写出
内部(不包括边界)时,直接写出![]() 的取值范围.
的取值范围.
(3)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,在运动过程中,是否存在某时刻使过
,在运动过程中,是否存在某时刻使过![]() 、
、![]() 、
、![]() 三点的圆与
三点的圆与![]() 三边中的一条边相切?若存在,请求出
三边中的一条边相切?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是( )
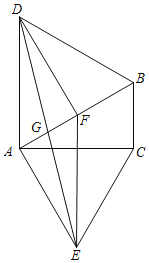
A.①③B.②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列四个应用题:①现有60个零件的加工任务,甲单独每小时可以加工4个零件,乙单独每小时可以加工6个零件.现甲乙两人合作,问两人开始工作几小时后还有20个零件没有加工?②甲乙两人从相距![]() 的两地同时出发,相向面行,甲的速度是
的两地同时出发,相向面行,甲的速度是![]() ,乙的速度是
,乙的速度是![]() ,问经过几小时后两人相遇后又相距
,问经过几小时后两人相遇后又相距![]() ?③甲乙两人从相距
?③甲乙两人从相距![]() 的两地相向面行,甲的速度是
的两地相向面行,甲的速度是![]() ,乙的速度是
,乙的速度是![]() ,如果甲先走了
,如果甲先走了![]() 后,乙再出发,问乙出发后几小时两人相遇?④甲乙两人从相距
后,乙再出发,问乙出发后几小时两人相遇?④甲乙两人从相距![]() 的两地同时出发,背向而行,甲的速度是
的两地同时出发,背向而行,甲的速度是![]() ,乙的速度是
,乙的速度是![]() ,问经过几小时后两人相距
,问经过几小时后两人相距![]() ?其中,可以用方程
?其中,可以用方程![]() 表述题目中对应数量关系的应用题序号是( )
表述题目中对应数量关系的应用题序号是( )
A.①②③④B.①③④C.②③④D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为矩形ABCD的边BC长上的一点,作DF⊥AE于点F,且满足DF=AB.下面结论:①△DEF≌△DEC;②S△ABE = S△ADF;③AF=AB;④BE=AF.其中正确的结论是( )
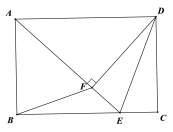
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
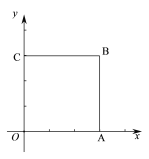
【题目】如图,在平面直角坐标系xOy中,正方形OABC的顶点A,C分别在x轴,y轴上,OA=3.
(1)求直线OB的表达式;
(2)若直线y=x+b与该正方形有两个公共点,请直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B两点,所表示的数分别为a、a+4,A点以每秒3个单位长度的速度向正方向运动,同时B点以每秒1个单位长度的速度也向正方向运动,设运动时间为t秒.
![]()
(1)运动前线段AB的长为 ,t秒后,A点运动的距离可表示为 , B点运动距离可表示为
(2)当t为何值时,A、B两点重合,并求出此时A点所表示的数(用含有a的式子表示);
(3)在上述运动的过程中,若P为线段AB的中点,O为数轴的原点,当a=-8时,是否存在这样的值,使得线段PO=5,若存在,求出符合条件的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上有三点A、B、C,若用AB表示A、B两点的距离,AC表示A、C两点的距离,且AB=![]() AC,点A、点C对应的数是分别是a、c,且|a+40|+|c﹣20|=0.
AC,点A、点C对应的数是分别是a、c,且|a+40|+|c﹣20|=0.
![]()
(1)求BC的长.
(2)若点P、Q分别从A、C两点同时出发向左运动,速度分别为2个单位长度每秒、5个单位长度每秒,则运动了多少秒时,Q到B的距离与P到B的距离相等?
(3)若点P、Q仍然以(2)中的速度分别从A、C两点同时出发向左运动,2秒后,动点R从A点出发向右运动,点R的速度为1个单位长度每秒,点M为线段PR的中点,点N为线段RQ的中点,点R运动了多少秒时恰好满足MN+AQ=31;并求出此时R点所对应的数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com