
����Ŀ����֪�����ĸ�Ӧ���⣺������60������ļӹ�������ÿСʱ���Լӹ�4��������ҵ���ÿСʱ���Լӹ�6�����.�ּ������˺����������˿�ʼ������Сʱ����20�����û�мӹ����ڼ������˴����![]() ������ͬʱ�������������У����ٶ���
������ͬʱ�������������У����ٶ���![]() ���ҵ��ٶ���
���ҵ��ٶ���![]() ���ʾ�����Сʱ�����������������
���ʾ�����Сʱ�����������������![]() ���ۼ������˴����
���ۼ������˴����![]() �������������У����ٶ���
�������������У����ٶ���![]() ���ҵ��ٶ���
���ҵ��ٶ���![]() �������������
�������������![]() �����ٳ��������ҳ�����Сʱ�����������ܼ������˴����
�����ٳ��������ҳ�����Сʱ�����������ܼ������˴����![]() ������ͬʱ������������У����ٶ���
������ͬʱ������������У����ٶ���![]() ���ҵ��ٶ���
���ҵ��ٶ���![]() ���ʾ�����Сʱ���������
���ʾ�����Сʱ���������![]() �����У������÷���
�����У������÷���![]() ������Ŀ�ж�Ӧ������ϵ��Ӧ��������ǣ� ��
������Ŀ�ж�Ӧ������ϵ��Ӧ��������ǣ� ��
A.�٢ڢۢ�B.�٢ۢ�C.�ڢۢ�D.�٢�
���𰸡�B
��������
�ٸ��ݼĹ�����+�ҵĹ�����+δ��ɵĹ�����=�ܵĹ���������xСʱ����20�����û�мӹ����ݴ��з��̽��
�ڸ��ݼ���ʻ��·��+����ʻ��·��=��·��+����������·�̣���xСʱ�����������20km���ݴ��з��̽��
�����ݼ�����ʻ��·�̺�+�����ߵ�·��=��·�̣���xСʱ�������ݴ��з��̽��
�ܸ��ݼ������˵ľ���+���Ҹ�����ʻ��·��=��·�̣�����ʻxСʱ���ݴ��з��̽��.
����xСʱ����20�����û�мӹ�����������ã�![]() ���ʢ���ȷ��
���ʢ���ȷ��
����xСʱ�����������20km����������ã�![]() ���ʢڴ���
���ʢڴ���
�ۼ�������![]() �����ٳ��������ҳ�����xСʱ������������������ã�
�����ٳ��������ҳ�����xСʱ������������������ã�![]() ���ʢ���ȷ��
���ʢ���ȷ��
�ܾ���xСʱ���������![]() ����������ã�
����������ã�![]() ���ʢ���ȷ.
���ʢ���ȷ.
��ˣ���ȷ���Ǣ٢ۢ�.
��ѡ��B.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С����Ƶġ���ƽ���ı���![]() ��ʹ
��ʹ![]() ��
��![]() ��������ͼ���̣�
��������ͼ���̣�
��������ͼ������![]() ��
��
����![]() �������Ϸֱ��ȡ
�������Ϸֱ��ȡ![]() ��
��![]() ��
��
���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶�������Ե�
��Ϊ�뾶�������Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶�����������ཻ�ڵ�
��Ϊ�뾶�����������ཻ�ڵ�![]() ��
��
������![]() ��
��![]() ��
��
���ı���![]() Ϊ��������ƽ���ı��Σ�
Ϊ��������ƽ���ı��Σ�
����С����Ƶ���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤����
֤���� ![]()
![]() ______��
______��![]() ______��
______��
![]() �ı���
�ı���![]() ��ƽ���ı��Σ���______���������������ݣ���
��ƽ���ı��Σ���______���������������ݣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
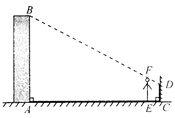
����Ŀ��С��������̫�������¥�ߣ�������Ƥ������һ��¥�£����ֶ���ǽ�����ⶰ¥��Ӱ�ӣ��������������������һ�ֲ����������������������£���ʾ��ͼ��С�����ƶ��߹۲죬����վ����E��ʱ������ʹ�Լ�����ǽ�ϵ�Ӱ�����ⶰ¥����ǽ�ϵ�Ӱ���ص����Ҹ߶�ǡ����ͬ����ʱ�����С������ǽ�ϵ�Ӱ�Ӹ߶�CD��1.2m��CE��0.8m��CA��30m����A��E��C��ͬһֱ���ϣ�����֪С��������EF��1.7m�������С�����¥��AB�������ȷ��0.1m����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
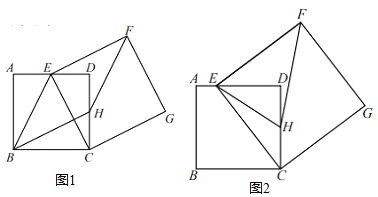
����Ŀ����ͼ�������� ABCD �У�AB��4���� EΪ��AD��һ���㣬���� CE���� CEΪ�ߣ���������CEFG����D��F��CE����ֱ�ߵ�ͬ�ࣩ��HΪCD�е㣬���� FH��
��1����ͼ 1������BE��BH�����ı��� BEFH Ϊƽ���ı��Σ����ı��� BEFH ���ܳ���
��2����ͼ 2������ EH���� AE��1������EHF �������
��3��ֱ��д����E���˶������У�HF����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����a1��a2��a3��a4��a5��ƽ������m����a1��a2��a3��a4��a5��0��������a1��a2��a3����3��a4��a5��ƽ��������λ���ֱ���_____��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪m��n��ʵ�����������㡰*��Ϊ��m*n��mn+n��
��1���ֱ���4*����2����4*![]() ��ֵ��
��ֵ��
��2��������x�ķ���x*��a*x������![]() ��������ȵ�ʵ��������ʵ��a��ֵ��
��������ȵ�ʵ��������ʵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
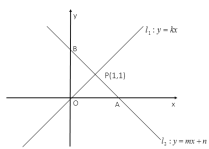
����Ŀ����ͼ��ֱ��l1��y=kx��ֱ��l2��y=mx+n�ཻ�ڵ�P(1,1)����ֱ��l2��x�ᣬy��ֱ������A��B���㣬��POA�������1��
��1������POB�������
��2��ֱ��д��kx>mx+n�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�MΪ��CB�ӳ�����һ�㣬����A��ֱ��AM�����BAM=������B����ֱ��AM�ĶԳƵ�Ϊ��E������AE��DE��DE��AM�ڵ�N��
�У�MΪ��CB�ӳ�����һ�㣬����A��ֱ��AM�����BAM=������B����ֱ��AM�ĶԳƵ�Ϊ��E������AE��DE��DE��AM�ڵ�N��
��1�������ⲹȫͼ�Σ�����=30��ʱ�� ֱ��д����AND�Ķ�����
��2�����������仯ʱ����AND�Ķ����Ƿ����仯��˵�����ɣ�
��3��̽���߶�AN��EN��DN��������ϵ����֤����


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2��5ax��4��x����A��B���㣨��Aλ�ڵ�B����ࣩ����y���ڵ�C������C��CD��AB�����������ڵ�D������AC��AD��AD��y���ڵ�E����AC=CD������A������AF��y���ڵ�F��ABƽ�֡�EAF��
��1���������ߵĶԳ������� ����
��2����������ߵĽ���ʽ��
��3������P��������λ�ڵ�������ͼ����һ���㣬����APF���S��APF�����ֵ���Լ���ʱ��P�����ꣻ
��4����M���߶�AB��һ�㣨�����A��B�غϣ�����N���߶�AD��һ�㣨�����A��D�غϣ��������߶γ���֮�ͣ�MN+MD����Сֵ���� ����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com