
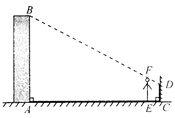
【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图①,在![]() ABCD中,AB=10cm,BC=4cm,∠BCD=120°,CE平分∠BCD交AB于点E.点P从A点出发,沿AB方向以1cm/s的速度运动,连接CP,将△PCE绕点C逆时针旋转60°,使CE与CB重合,得到△QCB,连接PQ.
ABCD中,AB=10cm,BC=4cm,∠BCD=120°,CE平分∠BCD交AB于点E.点P从A点出发,沿AB方向以1cm/s的速度运动,连接CP,将△PCE绕点C逆时针旋转60°,使CE与CB重合,得到△QCB,连接PQ.
(1)求证:△PCQ是等边三角形;
(2)如图②,当点P在线段EB上运动时,△PBQ的周长是否存在最小值?若存在,求
出△PBQ周长的最小值;若不存在,请说明理由;
(3)如图③,当点P在射线AM上运动时,是否存在以点P、B、Q为顶点的直角三角形?
若存在,求出此时t的值;若不存在,请说明理由.


(1) (2)

(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,A, B是直线l上的两点,点B关于AD的对称点为M,连接![]() 交AD于F点.
交AD于F点.
(1)若![]() ,如图,
,如图,
①依题意补全图形;
②判断MF与FC的数量关系是 ;

(2)如图,当![]() 时,
时,![]() ,CD的延长线相交于点E,取
,CD的延长线相交于点E,取![]() E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.
E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
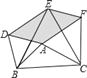
【题目】如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题:
(1)四边形ADEF是什么四边形?
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,BC=6,点E是AD边上一点,∠ABE=30°,BE=DE,连接BD.动点M从点E出发沿射线ED运动,过点M作MN∥BD交直线BE于点N.
(1)如图1,当点M在线段ED上时,求证:MN=![]() EM;
EM;
(2)设MN长为x,以M、N、D为顶点的三角形面积为y,求y关于x的函数关系式;
(3)当点M运动到线段ED的中点时,连接NC,过点M作MF⊥NC于F,MF交对角线BD于点G(如图2),求线段MG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
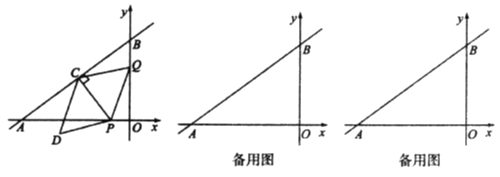
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴负方向以每秒1个单位长度的速度运动,同时动点
轴负方向以每秒1个单位长度的速度运动,同时动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向以每秒2个单位长度的速度运动,过点
方向以每秒2个单位长度的速度运动,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,以
,以![]() 、
、![]() 为邻边构造平行四边形
为邻边构造平行四边形![]() ,设点
,设点![]() 运动的时间为
运动的时间为![]() s.
s.
(1)当点![]() 在线段
在线段![]() 上时,用含
上时,用含![]() 的代数式表示
的代数式表示![]() 、
、![]() 的长.
的长.
(2)在运动过程中,①当点![]() 落在
落在![]() 轴上时,求出满足条件的
轴上时,求出满足条件的![]() 的值;②当点
的值;②当点![]() 落在
落在![]() 内部(不包括边界)时,直接写出
内部(不包括边界)时,直接写出![]() 的取值范围.
的取值范围.
(3)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,在运动过程中,是否存在某时刻使过
,在运动过程中,是否存在某时刻使过![]() 、
、![]() 、
、![]() 三点的圆与
三点的圆与![]() 三边中的一条边相切?若存在,请求出
三边中的一条边相切?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
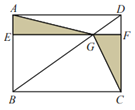
【题目】如图,矩形ABCD中,点 E、F 分别在AB、CD上,EF∥BC,EF交BD于点G.若EG=5,DF=2,则图中两块阴影部分的面积之和为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列四个应用题:①现有60个零件的加工任务,甲单独每小时可以加工4个零件,乙单独每小时可以加工6个零件.现甲乙两人合作,问两人开始工作几小时后还有20个零件没有加工?②甲乙两人从相距![]() 的两地同时出发,相向面行,甲的速度是
的两地同时出发,相向面行,甲的速度是![]() ,乙的速度是
,乙的速度是![]() ,问经过几小时后两人相遇后又相距
,问经过几小时后两人相遇后又相距![]() ?③甲乙两人从相距
?③甲乙两人从相距![]() 的两地相向面行,甲的速度是
的两地相向面行,甲的速度是![]() ,乙的速度是
,乙的速度是![]() ,如果甲先走了
,如果甲先走了![]() 后,乙再出发,问乙出发后几小时两人相遇?④甲乙两人从相距
后,乙再出发,问乙出发后几小时两人相遇?④甲乙两人从相距![]() 的两地同时出发,背向而行,甲的速度是
的两地同时出发,背向而行,甲的速度是![]() ,乙的速度是
,乙的速度是![]() ,问经过几小时后两人相距
,问经过几小时后两人相距![]() ?其中,可以用方程
?其中,可以用方程![]() 表述题目中对应数量关系的应用题序号是( )
表述题目中对应数量关系的应用题序号是( )
A.①②③④B.①③④C.②③④D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com