
【题目】如图①,在![]() ABCD中,AB=10cm,BC=4cm,∠BCD=120°,CE平分∠BCD交AB于点E.点P从A点出发,沿AB方向以1cm/s的速度运动,连接CP,将△PCE绕点C逆时针旋转60°,使CE与CB重合,得到△QCB,连接PQ.
ABCD中,AB=10cm,BC=4cm,∠BCD=120°,CE平分∠BCD交AB于点E.点P从A点出发,沿AB方向以1cm/s的速度运动,连接CP,将△PCE绕点C逆时针旋转60°,使CE与CB重合,得到△QCB,连接PQ.
(1)求证:△PCQ是等边三角形;
(2)如图②,当点P在线段EB上运动时,△PBQ的周长是否存在最小值?若存在,求
出△PBQ周长的最小值;若不存在,请说明理由;
(3)如图③,当点P在射线AM上运动时,是否存在以点P、B、Q为顶点的直角三角形?
若存在,求出此时t的值;若不存在,请说明理由.


(1) (2)

(3)
【答案】(1)证明见解析;(2)存在,理由见解析;(3)t为2s或者14s.
【解析】分析:(1)根据旋转的性质,证明△PCE≌△QCB,然后根据全等三角形的性质和等边三角形的判定证明即可;
(2)利用平行四边形的性质证得△BCE为等边三角形,然后根据全等三角形的性质得到△PBQ的周长为4+CP,然后垂线段最短可由直角三角形的性质求解即可;
(3)根据点的移动的距离,分类讨论求解即可.
详解:(1)∵旋转
∴△PCE≌△QCB
∴CP=CQ,∠PCE =∠QCB,
∵∠BCD=120°,CE平分∠BCD,
∴∠PCQ=60°,
∴∠PCE +∠QCE=∠QCB+∠QCE=60°,
∴△PCQ为等边三角形.
(2)存在
∵CE平分∠BCD,
∴∠BCE=![]() ,
,
∵在平行四边形ABCD 中,
∴AB∥CD
∴∠ABC=180°﹣120°=60°
∴△BCE为等边三角形
∴BE=CB=4
∵旋转
∴△PCE≌△QCB
∴EP=BQ,
∴C△PBQ=PB+BQ+PQ
=PB+EP+PQ
=BE+PQ
=4+CP
∴CP⊥AB时,△PBQ周长最小
当CP⊥AB时,CP=BCsin60°=![]()
∴△PBQ周长最小为4+![]()
(3)①当点B与点P重合时,P,B,Q不能构成三角形
②当0≤t<6时,由旋转可知,
∠CPE=∠CQB,
∠CPQ=∠CPB+∠BPQ=60°
则:∠BPQ+∠CQB=60°,
又∵∠QPB+∠PQC+∠CQB+∠PBQ=180°
∴∠CBQ=180°—60°—60°=60°
∴∠QBP=60°,∠BPQ<60°,
所以∠PQB可能为直角
由(1)知,△PCQ为等边三角形,
∴∠PBQ=60°,∠CQB=30°
∵∠CQB=∠CPB
∴∠CPB=30°
∵∠CEB=60°,
∴∠ACP=∠APC=30°
∴PA=CA=4,
所以AP=AE-EP=6-4=2
所以t=2![]() s
s
③当6<t<10时,由∠PBQ=120°>90°,所以不存在
④当t>10时,由旋转得:∠PBQ=60°,由(1)得∠CPQ=60°
∴∠BPQ=∠CPQ+∠BPC=60°+∠BPC,
而∠BPC>0°,
∴∠BPQ>60°
∴∠BPQ=90°,从而∠BCP=30°,
∴BP=BC=4
所以AP=14cm
所以t=14s
综上所述:t为2s或者14s时,符合题意。


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=3
,AH=3![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,将线段EF绕点F旋转,使点E落在BE上的点G处,连接CG.
(1)证明:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积;
(3)试探究当线段AB与BC满足什么数量关系时,BG=CG,请写出你的探究过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与化简
(1)计算:(6m2+4m﹣3)+2(2m2﹣4m+1);
(2)先化简,再求值.4xy﹣[(x2+5xy﹣y2)﹣2(x2+3xy﹣![]() y2)],其中:x=﹣1,y=2.
y2)],其中:x=﹣1,y=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线![]() 经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是_____.
经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作平行四边形![]() ,使
,使![]() ,
,![]() ,”的作图过程.
,”的作图过程.
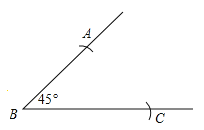
作法:如图,①作![]() ;
;
②在![]() 的两边上分别截取
的两边上分别截取![]() ,
,![]() ;
;
③以点![]() 为圆心,
为圆心,![]() 长为半径画弧,以点
长为半径画弧,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,两弧相交于点
长为半径画弧,两弧相交于点![]() ;
;
④连接![]() ,
,![]() .
.
则四边形![]() 为所求作的平行四边形.
为所求作的平行四边形.
根据小东设计的作图过程:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明: ![]()
![]() ______,
______,![]() ______,
______,
![]() 四边形
四边形![]() 是平行四边形.(______)(填推理的依据).
是平行四边形.(______)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
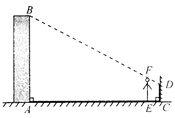
【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com