
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
【答案】(1) 众数为15;(2) 3,4,15;8;(3) 月销售额定为18万,有一半左右的营业员能达到销售目标.
【解析】
根据数据可得到落在第四组、第六组的个数分别为3个、4个,所以a=3,b=4,再根据数据可得15出现了5次,出现次数最多,所以众数c=15;
从频数分布表中可以看出月销售额不低于25万元的营业员有8个,所以本小题答案为:8;
本题是考查中位数的知识,根据中位数可以让一半左右的营业员达到销售目标.
解:(1)在![]() 范围内的数据有3个,在
范围内的数据有3个,在![]() 范围内的数据有4个,
范围内的数据有4个,
15出现的次数最大,则众数为15;
(2)月销售额不低于25万元为后面三组数据,即有8位营业员获得奖励;
故答案为3,4,15;8;
(3)想让一半左右的营业员都能达到销售目标,我认为月销售额定为18万合适.
因为中位数为18,即大于18与小于18的人数一样多,
所以月销售额定为18万,有一半左右的营业员能达到销售目标.


科目:初中数学 来源: 题型:
【题目】如图1,在一张长方形纸条上画一条数轴.

(1)若折叠纸条使数轴上表示﹣1的点与表示5的点重合,则折痕与数轴的交点表示的数是 ;
(2)如果数轴上两点之间的距离为6+m2(m为常数),这两点经过(1)的折叠方式后折痕与数轴的交点与(1)中的交点相同,求左边这个点表示的数;(用含m的代数式表示)
(3)如图2,若将此纸条沿A,B处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折n次后,再将其展开,求最右端的折痕与数轴的交点表示的数.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在正是草莓热销的季节,某水果零售商店分两批次从批发市场共购进草莓40箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款700元.
(1)设第一、二次购进草莓的箱数分别为a箱、b箱,求a,b的值;
(2)若商店对这40箱草莓先按每箱60元销售了x箱,其余的按每箱35元全部售完.
①求商店销售完全部草莓所获利润y(元)与x(箱)之间的函数关系式;
②当x的值至少为多少时,商店才不会亏本.(注:按整箱出售,利润=销售总收入-进货总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“分组合作学习”已成为推动课堂教学改革,打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析,统计图如下:

请结合图中信息解答下列问题:
(1)求出随机抽取调查的学生人数;
(2)补全分组后学生学习兴趣的条形统计图;
(3)分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.

(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点![]() 表示,小红家用点
表示,小红家用点![]() 表示,小刚家用点
表示,小刚家用点![]() 表示)
表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油1.5升,那么这辆货车此次送货共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
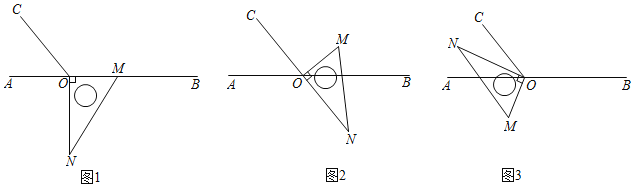
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=2∠AOC,将一直角三角板的直角顶点放在点O处,边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转45°至图2的位置,此时∠MOC= °;
(2)将图1中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转一周的过程中,若三角板绕点O按5°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() ABCD中,AB=10cm,BC=4cm,∠BCD=120°,CE平分∠BCD交AB于点E.点P从A点出发,沿AB方向以1cm/s的速度运动,连接CP,将△PCE绕点C逆时针旋转60°,使CE与CB重合,得到△QCB,连接PQ.
ABCD中,AB=10cm,BC=4cm,∠BCD=120°,CE平分∠BCD交AB于点E.点P从A点出发,沿AB方向以1cm/s的速度运动,连接CP,将△PCE绕点C逆时针旋转60°,使CE与CB重合,得到△QCB,连接PQ.
(1)求证:△PCQ是等边三角形;
(2)如图②,当点P在线段EB上运动时,△PBQ的周长是否存在最小值?若存在,求
出△PBQ周长的最小值;若不存在,请说明理由;
(3)如图③,当点P在射线AM上运动时,是否存在以点P、B、Q为顶点的直角三角形?
若存在,求出此时t的值;若不存在,请说明理由.


(1) (2)

(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
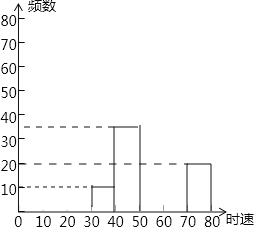
【题目】随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30﹣40含起点值30,不含终点值40),得到其频数及频率如表:
数据段 | 频数 | 频率 |
30﹣40 | 10 | 0.05 |
40﹣50 | 36 | c |
50﹣60 | a | 0.39 |
60﹣70 | b | d |
70﹣80 | 20 | 0.10 |
总计 | 200 | 1 |
(1)表中a、b、c、d分别为:a= ; b= ; c= ; d=
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
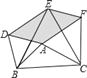
【题目】如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题:
(1)四边形ADEF是什么四边形?
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com