
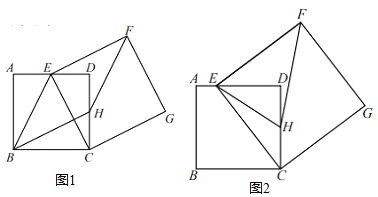
【题目】如图,正方形 ABCD 中,AB=4,点 E为边AD上一动点,连接 CE,以 CE为边,作正方形CEFG(点D、F在CE所在直线的同侧),H为CD中点,连接 FH.
(1)如图 1,连接BE,BH,若四边形 BEFH 为平行四边形,求四边形 BEFH 的周长;
(2)如图 2,连接 EH,若 AE=1,求△EHF 的面积;
(3)直接写出点E在运动过程中,HF的最小值.
【答案】(1)8![]() ;(2)
;(2)![]() ;(3)3
;(3)3![]() .
.
【解析】
(1)由平行四边形的性质和正方形的性质可得EC=EF=BH,BC=DC,可证Rt△BHC≌Rt△CED,可得CH=DE,由“SAS”可证BE=EC,可得BE=EF=HF=BH=EC,由勾股定理可求BH的长,即可求四边形BEFH的周长;
(2)连接DF,过点F作FM⊥AD,交AD延长线于点M,由“AAS”可证△EFM≌△CED,可得CD=EM=4,DE=FM=3,由三角形面积公式可求解;
(3)过点F作FN⊥CD的延长线于点N,设AE=x=DM,则DE=4-x=FM,NH=4-x+2=6-x,由勾股定理可求HF的长,由二次函数的性质可求HF的最小值.
解:(1)∵四边形BEFH为平行四边形
∴BE=HF,BH=EF
∵四边形EFGC,四边形ABCD都是正方形
∴EF=EC,BC=CD=4=AD
∴BH=EC,且BC=CD
∴Rt△BHC≌Rt△CED(HL)
∴CH=DE
∵H为CD中点,
∴CH=2=DE
∴AE=AD-DE=2=DE,且AB=CD,∠BAD=∠ADC=90°
∴Rt△ABE≌Rt△DCE(SAS)
∴BE=EC
∴BE=EF=HF=BH=EC
∵CH=2,BC=4
∴BH=![]() =
=![]() =2
=2![]()
∴四边形BEFH的周长=BE+BH+EF+FH=8![]() ;
;
(2)如图2,连接DF,过点F作FM⊥AD,交AD延长线于点M,
∵AE=1,
∴DE=3
∵∠FEM+∠CEM=90°,∠CEM+∠ECD=90°
∴∠FEM=∠ECD,且CE=EF,∠EDC=∠EMF=90°
∴△EFM≌△CED(AAS)
∴CD=EM=4,DE=FM=3,
∴DM=1,
∴S△EFH=S△EFD+S△EDH+S△DHF=![]() ×3×3+
×3×3+![]() ×3×2+
×3×2+![]() ×2×1=
×2×1=![]() ;
;
(3)如图3,过点F作FN⊥CD的延长线于点N,
由(2)可知:△EFM≌△CED
∴CD=EM,DE=FM,
∴CD=AD=EM,
∴AE=DM,
设AE=x=DM,则DE=4-x=FM,
∵FN⊥CD,FM⊥AD,ND⊥AD
∴四边形FNDM是矩形
∴FN=DM=x,FM=DN=4-x
∴NH=4-x+2=6-x
在Rt△NFH中,HF=![]() =
=![]() =
=![]()
∴当x=3时,HF有最小值=![]() =3
=3![]() .
.
故答案为:(1)8![]() ;(2)
;(2)![]() ;(3)3
;(3)3![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
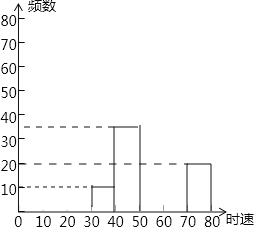
【题目】随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30﹣40含起点值30,不含终点值40),得到其频数及频率如表:
数据段 | 频数 | 频率 |
30﹣40 | 10 | 0.05 |
40﹣50 | 36 | c |
50﹣60 | a | 0.39 |
60﹣70 | b | d |
70﹣80 | 20 | 0.10 |
总计 | 200 | 1 |
(1)表中a、b、c、d分别为:a= ; b= ; c= ; d=
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
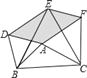
【题目】如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题:
(1)四边形ADEF是什么四边形?
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?
查看答案和解析>>
科目:初中数学 来源: 题型:
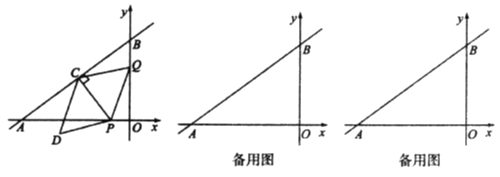
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴负方向以每秒1个单位长度的速度运动,同时动点
轴负方向以每秒1个单位长度的速度运动,同时动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向以每秒2个单位长度的速度运动,过点
方向以每秒2个单位长度的速度运动,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,以
,以![]() 、
、![]() 为邻边构造平行四边形
为邻边构造平行四边形![]() ,设点
,设点![]() 运动的时间为
运动的时间为![]() s.
s.
(1)当点![]() 在线段
在线段![]() 上时,用含
上时,用含![]() 的代数式表示
的代数式表示![]() 、
、![]() 的长.
的长.
(2)在运动过程中,①当点![]() 落在
落在![]() 轴上时,求出满足条件的
轴上时,求出满足条件的![]() 的值;②当点
的值;②当点![]() 落在
落在![]() 内部(不包括边界)时,直接写出
内部(不包括边界)时,直接写出![]() 的取值范围.
的取值范围.
(3)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,在运动过程中,是否存在某时刻使过
,在运动过程中,是否存在某时刻使过![]() 、
、![]() 、
、![]() 三点的圆与
三点的圆与![]() 三边中的一条边相切?若存在,请求出
三边中的一条边相切?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点 E、F 分别在AB、CD上,EF∥BC,EF交BD于点G.若EG=5,DF=2,则图中两块阴影部分的面积之和为______.
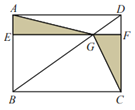
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是( )
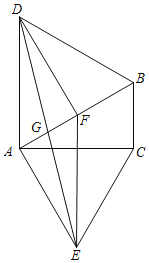
A.①③B.②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列四个应用题:①现有60个零件的加工任务,甲单独每小时可以加工4个零件,乙单独每小时可以加工6个零件.现甲乙两人合作,问两人开始工作几小时后还有20个零件没有加工?②甲乙两人从相距![]() 的两地同时出发,相向面行,甲的速度是
的两地同时出发,相向面行,甲的速度是![]() ,乙的速度是
,乙的速度是![]() ,问经过几小时后两人相遇后又相距
,问经过几小时后两人相遇后又相距![]() ?③甲乙两人从相距
?③甲乙两人从相距![]() 的两地相向面行,甲的速度是
的两地相向面行,甲的速度是![]() ,乙的速度是
,乙的速度是![]() ,如果甲先走了
,如果甲先走了![]() 后,乙再出发,问乙出发后几小时两人相遇?④甲乙两人从相距
后,乙再出发,问乙出发后几小时两人相遇?④甲乙两人从相距![]() 的两地同时出发,背向而行,甲的速度是
的两地同时出发,背向而行,甲的速度是![]() ,乙的速度是
,乙的速度是![]() ,问经过几小时后两人相距
,问经过几小时后两人相距![]() ?其中,可以用方程
?其中,可以用方程![]() 表述题目中对应数量关系的应用题序号是( )
表述题目中对应数量关系的应用题序号是( )
A.①②③④B.①③④C.②③④D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,正方形OABC的顶点A,C分别在x轴,y轴上,OA=3.
(1)求直线OB的表达式;
(2)若直线y=x+b与该正方形有两个公共点,请直接写出b的取值范围.
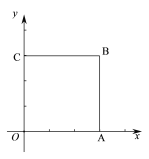
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,直线y=![]() x+b与直线y=
x+b与直线y=![]() x交于点A(m,1).与y轴交于点B
x交于点A(m,1).与y轴交于点B
(1)求m的值和点B的坐标;
(2)若点C在y轴上,且△ABC的面积是1,请直接写出点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com