
【题目】如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是( )
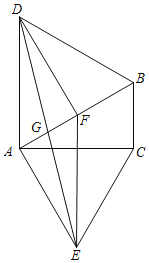
A.①③B.②④C.①③④D.②③④
【答案】C
【解析】
根据直角三角形斜边上的中线等于斜边的一半,可得FA=FC,根据等边三角形的性质可得EA=EC,根据线段垂直平分线的判定可得EF是线段AC的垂直平分线;根据条件及等边三角形的性质可得∠DFA=∠EAF=90°,DA⊥AC,从而得到DF∥AE,DA∥EF,可得到四边形ADFE为平行四边形而不是菱形;根据平行四边形的对角线互相平分可得AD=AB=2AF=4AG;易证DB=DA=EF,∠DBF=∠EFA=60°,BF=FA,即可得到△DBF≌△EFA.
连接FC,如图所示:
∵∠ACB=90°,F为AB的中点,
∴FA=FB=FC,
∵△ACE是等边三角形,
∴EA=EC,
∵FA=FC,EA=EC,
∴点F、点E都在线段AC的垂直平分线上,
∴EF垂直平分AC,即EF⊥AC;
∵△ABD和△ACE都是等边三角形,F为AB的中点,
∴DF⊥AB即∠DFA=90°,BD=DA=AB=2AF,∠DBA=∠DAB=∠EAC=∠ACE=60°.
∵∠BAC=30°,
∴∠DAC=∠EAF=90°,
∴∠DFA=∠EAF=90°,DA⊥AC,
∴DF∥AE,DA∥EF,
∴四边形ADFE为平行四边形而不是菱形;
∵四边形ADFE为平行四边形,
∴DA=EF,AF=2AG,
∴BD=DA=EF,DA=AB=2AF=4AG;
在△DBF和△EFA中, ,
,
∴△DBF≌△EFA(SAS);
综上所述:①③④正确,
故选:C.



科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH.
(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);
(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),
①试用含α的代数式表示∠HAE;
②求证:HE=HG;
③四边形EFGH是什么四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
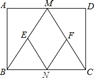
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)填空:当AB:AD= 时,四边形MENF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
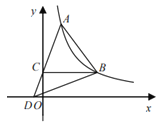
【题目】如图,点A、B都在反比例函数y=![]() (x>0)的图像上,过点B作BC∥x轴交y轴于点C,连接AC并延长交x轴于点D,连接BD,DA=3DC,S△ABD=6.则k的值为_______.
(x>0)的图像上,过点B作BC∥x轴交y轴于点C,连接AC并延长交x轴于点D,连接BD,DA=3DC,S△ABD=6.则k的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
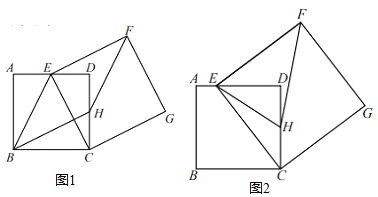
【题目】如图,正方形 ABCD 中,AB=4,点 E为边AD上一动点,连接 CE,以 CE为边,作正方形CEFG(点D、F在CE所在直线的同侧),H为CD中点,连接 FH.
(1)如图 1,连接BE,BH,若四边形 BEFH 为平行四边形,求四边形 BEFH 的周长;
(2)如图 2,连接 EH,若 AE=1,求△EHF 的面积;
(3)直接写出点E在运动过程中,HF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为-3,0,1,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M,点N的距离相等,那么x的值是______;
(2)数轴上是否存在点P,使点P到点M,点N的距离之和是5?若存在,请直接写出x的值;若不存在,请说明理由.
(3)如果点P以每分钟3个单位长度的速度从点O向左运动时,点M和点N分别以每分钟1个单位长度和每分钟4个单位长度的速度也向左运动,且三点同时出发,那么几分钟时点P到点M,点N的距离相等.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n是实数,定义运算“*”为:m*n=mn+n.
(1)分别求4*(﹣2)与4*![]() 的值;
的值;
(2)若关于x的方程x*(a*x)=﹣![]() 有两个相等的实数根,求实数a的值.
有两个相等的实数根,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化,促进学生全面发展.我市某区教育局在全区中小学开展“书法、武术、黄梅戏进校园”活动。今年3月份,该区某校举行了“黄梅戏”演唱比赛,比赛成绩评定为A,B,C,D,E五个等级,该校部分学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图,请根据图中信息,解答下列问题.

(1)求该校参加本次“黄梅戏”演唱比赛的学生人数;
(2)求扇形统计图B等级所对应扇形的圆心角度数;
(3)已知A等级的4名学生中有1名男生,3名女生,现从中任意选取2名学生作为全校训练的示范者,请你用列表法或画树状图的方法,求出恰好选1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
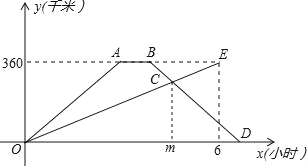
【题目】(8分)快、慢两车分别从相距360千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距各自出发地的路程y(千米)与出发后所用的时间x(小时)的关系如图.
请结合图象信息解答下列问题:
(1)慢车的速度是 千米/小时,快车的速度是 千米/小时;
(2)求m的值,并指出点C的实际意义是什么?
(3)在快车按原路原速返回的过程中,快、慢两车相距的路程为150千米时,慢车行驶了多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com