
����Ŀ����֪����������M��O��N��Ӧ�����ֱ�Ϊ��3��0��1����PΪ����������һ�㣬���Ӧ����Ϊx��
(1)�����P����M����N�ľ�����ȣ���ôx��ֵ��______��
(2)�������Ƿ���ڵ�P��ʹ��P����M����N�ľ���֮����5�������ڣ���ֱ��д��x��ֵ���������ڣ���˵�����ɣ�
(3)�����P��ÿ����3����λ���ȵ��ٶȴӵ�O�����˶�ʱ����M�͵�N�ֱ���ÿ����1����λ���Ⱥ�ÿ����4����λ���ȵ��ٶ�Ҳ�����˶���������ͬʱ��������ô������ʱ��P����M����N�ľ������.��ֱ��д���𰸣�
���𰸡���1��![]() ����2��x=
����2��x=![]() ��
��![]() ����3��
����3��![]() ���ӻ�t=2����ʱ��P����M����N�ľ�����ȣ�
���ӻ�t=2����ʱ��P����M����N�ľ�����ȣ�
��������
��1����������M��O��N��Ӧ�������ó�NM���е�Ϊ��x=��-3+1����2����������ɣ�
��2������P����N���Ҳ����M�����ֱ�������ɣ�
��3���ֱ���ݢٵ���M�͵�N�ڵ�Pͬ��ʱ���ڵ���M�͵�N�ڵ�P����ʱ������ɣ�
�⣺��1����M��O��N��Ӧ�����ֱ�Ϊ-3��0��1����P����M����N�ľ�����ȣ�
��x��ֵ��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2�����ڷ�������ĵ�P��
�ߵ�MΪ-3����NΪ1�����P��Ϊ���������
�ٵ�P��N���Ҳ࣬��
![]() ����ã�
����ã�![]() ��
��
�ڵ�P��M����࣬��
![]() ����ã�
����ã�![]() ��
��
��![]() .
.
��3�����˶�t����ʱ����P��Ӧ������-3t����M��Ӧ������-3-t����N��Ӧ������1-4t��
�ٵ���M�͵�N�ڵ�Pͬ��ʱ����ΪPM=PN�����Ե�M�͵�N�غϣ�
���ԣ�-3-t=1-4t��
���t��![]() ���������⣮
���������⣮
�ڵ���M�͵�N�ڵ�P����ʱ�������������
���1�������M�ڵ�N��࣬PM=-3t-��-3-t��=3-2t��PN=��1-4t��-��-3t��=1-t��
��ΪPM=PN������3-2t=1-t��
���t=2��
��ʱ��M��Ӧ������-5����N��Ӧ������-7����M�ڵ�N�Ҳ࣬���������⣬
��ȥ��
���2�������M�ڵ�N�Ҳ࣬PM=3t-t-3=2t-3��PN=-3t-��1-4t��=t-1��
��ΪPM=PN������2t-3=t-1��
���t=2��
��ʱ��M��Ӧ������-5����N��Ӧ������-7����M�ڵ�N�Ҳ࣬�������⣮
��������������ͬʱ������![]() ���ӻ�2����ʱ��P����M����N�ľ�����ȣ�
���ӻ�2����ʱ��P����M����N�ľ�����ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ϣ�A1��P�����ʾ�����ֱ�Ϊ1��3��A1��A2����O�Գƣ�A2��A3���ڵ�P�Գƣ�A3��A4���ڵ�O�Գƣ�A4��A5���ڵ�P�Գ������ι��ɣ����A15��ʾ������_____��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ԲO��ֱ��DE=10cm����ABC�У���ACB=90�㣬��ABC=30�㣬BC=10cm����ԲO��1cm/s���ٶȴ��ҵ����˶������˶������У�D��E��ʼ����ֱ��BC�ϣ����˶�ʱ��Ϊt��s������t=0��s��ʱ����ԲO����ABC���Ҳ࣬OC=6cm����ô����tΪ_____sʱ����ABC��һ������ֱ�����ԲO���ڵ�Բ���У�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=![]() ��x��2��2+1��ͼ����y������ƽ�Ƶõ�һ���º�����ͼ�����е�A��1��m����B��4��n��ƽ�ƺ�Ķ�Ӧ��ֱ�Ϊ��A'��B'�������߶�ABɨ�������Ϊ9��ͼ�е���Ӱ���֣�������ͼ��ĺ�������ʽ�ǣ�������
��x��2��2+1��ͼ����y������ƽ�Ƶõ�һ���º�����ͼ�����е�A��1��m����B��4��n��ƽ�ƺ�Ķ�Ӧ��ֱ�Ϊ��A'��B'�������߶�ABɨ�������Ϊ9��ͼ�е���Ӱ���֣�������ͼ��ĺ�������ʽ�ǣ�������

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
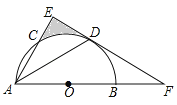
����Ŀ����ͼ��ABΪ��ԲO��ֱ����AC�ǡ�O��һ���ң�DΪ![]() ���е㣬��DE��AC����AB���ӳ����ڵ�F������DA��
���е㣬��DE��AC����AB���ӳ����ڵ�F������DA��
��1����֤��EFΪ��ԲO�����ߣ�
��2����DA=DF=![]() ������Ӱ����������������������ź�����
������Ӱ����������������������ź�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
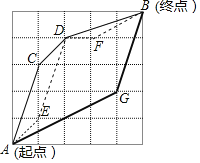
����Ŀ���μβμӻ�������ƻ����ٿػ�������5��5�����̸��ϴ�A��������B�㣬��ÿ��С�����Ϊ�����Σ����쵥λ�涨����������·��R1��R2��R2�����о�λ����ͼ�����ʾ��
·�� | ��� | ͼ�� | �о�λ�� |
��һ��·�� | R1 | �� | A��C��D��B |
�ڶ���·�� | R2 | �� | A��E��D��F��B |
������·�� | R3 | �� | A��G��B |
��֪A,B,C,D,E,F,G�ߵ�����ڸ��ߵĽ����ϣ�������֮���·����Ϊ�߶�.
(1)�ֱ���������·���ij�;
(2)���·����______ (д�����)����̵�·���� _______(д�����).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ��ţ�̣�����Ϊÿ��24Ԫ���涨�ۼ۲����ڽ��ۣ����ڵ��ۼ�Ϊÿ��36Ԫ��ÿ�¿�����60�䣮�г����鷢�֣�������ţ�̵��ۼ�ÿ����1Ԫ����ÿ�µ�����������10�䣬��ÿ��ţ�̽���xԪ(xΪ������)��ÿ�µ�����Ϊy�䣮
��1��д��y��x�м�ĺ�����ϵʽ���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������ζ��ۣ�����ʹÿ������ţ�̵����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��![]() x��˫����y��
x��˫����y��![]() ��k>0��x>0�����ڵ�A����ֱ��y��
��k>0��x>0�����ڵ�A����ֱ��y��![]() x����ƽ��4����λ���Ⱥ���y�ύ�ڵ�C����˫����y��
x����ƽ��4����λ���Ⱥ���y�ύ�ڵ�C����˫����y��![]() ��k>0��x>0�����ڵ�B����OA��3BC����k��ֵΪ��������
��k>0��x>0�����ڵ�B����OA��3BC����k��ֵΪ��������

A. 3 B. 6 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������AB�ĸ�Ϊ6m����������������һ��ͨ����CD��������֮��ĵ����M��B��M��D������һ��ֱ���ϣ�����ý����ﶥ��A������C�����Ƿֱ�Ϊ37���60�㣬��A���������C������Ϊ30�㣬��ͨ����CD�ĸ߶ȣ�����ȷ��0.01m��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com