Question

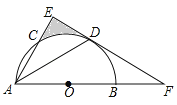
【题目】如图，AB为半圆O的直径，AC是⊙O的一条弦，D为的中点，作DE⊥AC，交AB的延长线于点F，连接DA．

（1）求证：EF为半圆O的切线；

（2）若DA=DF=，求阴影区域的面积．（结果保留根号和π）

Answer 1

【答案】（1）证明见解析；（2）﹣6π．

【解析】试题分析：（1）直接利用切线的判定方法结合圆心角定理分析得出OD⊥EF，即可得出答案；

（2）直接利用得出S△ACD=S△COD，再利用S阴影=S△AED﹣S扇形COD，求出答案．

试题解析：解：（1）连接OD，∵D为的中点，∴∠CAD=∠BAD，∵OA=OD，∴∠BAD=∠ADO，∴∠CAD=∠ADO，∵DE⊥AC，∴∠E=90°，∴∠CAD+∠EDA=90°，即∠ADO+∠EDA=90°，∴OD⊥EF，∴EF为半圆O的切线；

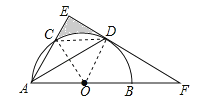
（2）连接OC与CD，∵DA=DF，∴∠BAD=∠F，∴∠BAD=∠F=∠CAD，又∵∠BAD+∠CAD+∠F=90°，∴∠F=30°，∠BAC=60°，∵OC=OA，∴△AOC为等边三角形，∴∠AOC=60°，∠COB=120°，∵OD⊥EF，∠F=30°，∴∠DOF=60°，在Rt△ODF中，DF=，∴OD=DFtan30°=6，在Rt△AED中，DA=，∠CAD=30°，∴DE=DAsin30°=，EA=DAcos30°=9．

∵∠COD=180°-∠AOC-∠DOF=60°，由CO=DO，∴△COD是等边三角形，∴∠OCD=60°，∴∠DCO=∠AOC=60°，∴CD∥AB．故S△ACD=S△COD，∴S阴影=S△AED﹣S扇形COD=×9×﹣=﹣6π．