【题目】如图，在矩形ABCD中，AB＝9，BC＝6，若矩形AEFG与矩形ABCD是位似图形且相似比为
，求C，F之间的距离．
【答案】C，F之间的距离为
【解析】试题分析：
如图，过点F作FH⊥BC于点H，连接CF，由已知容易求得EF=4，AE=6，从而可得CH=BC-BH=BC-EF=2，FH=BE=AB-AE=3，这样在Rt△CHF中，由勾股定理即可求得CF=
.
试题解析：
如图，过点F作FH⊥BC于点H，连接CF，
∴∠BHF=∠CFH=90°，
∵矩形AEFG与矩形ABCD是位似图形且相似比为
，AB＝9，BC＝6，
∴∠B=∠BEF=90°，AE=6，EF=4，
∴四边形BEFH是矩形，
∴BH=EF=4，FH=BE=AB-AE=3，
∴CH=BC-BH=6-4=2，
∴在Rt△CFH中，CF=
，即点C和点F之间的距离为
.
科目：初中数学 来源： 题型：
【题目】如图是一个玩具火车轨道，A点有个变轨开关，可以连接B或C．小圈轨道的周长是1.5米，大圈轨道的周长是3米．开始时，A连接C，火车从A点出发，按照顺时针方向再轨道上移动，同时变轨开关每隔一分钟变换一次轨道连接．若火车的速度是每分钟10米，则火车第10次回到A点时用了______分钟．
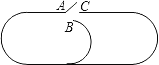
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为半圆O的直径，AC是⊙O的一条弦，D为
的中点，作DE⊥AC，交AB的延长线于点F，连接DA．
（1）求证：EF为半圆O的切线；
（2）若DA=DF=
，求阴影区域的面积．（结果保留根号和π）
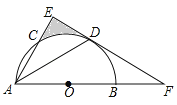
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某超市销售一种牛奶，进价为每箱24元，规定售价不低于进价．现在的售价为每箱36元，每月可销售60箱．市场调查发现：若这种牛奶的售价每降价1元，则每月的销量将增加10箱，设每箱牛奶降价x元(x为正整数)，每月的销量为y箱．
（1）写出y与x中间的函数关系式和自变量
的取值范围；
（2）超市如何定价，才能使每月销售牛奶的利润最大？最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC的顶点坐标分别为A（-2,1），B（-3,-2），C（1，-2）.把△ABC向上平移4个单位长度，再向右平移3个单位长度，得到△A′B′C′．
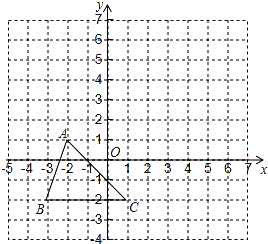
（1）在图中画出△A′B′C′，并写出点A′，B′，C′的坐标；
（2）连接A′C和A′A，求三角形AA′C的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y＝
x与双曲线y＝
（k>0，x>0）交于点A，将直线y＝
x向上平移4个单位长度后，与y轴交于点C，与双曲线y＝
（k>0，x>0）交于点B，若OA＝3BC，则k的值为（ ）
A. 3 B. 6 C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：
在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗？
小敏在思考问题时，有如下思路：连接AC．
结合小敏的思路作答：
（1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由，参考小敏思考问题的方法解决一下问题；
（2）如图2，在（1）的条件下，若连接AC，BD．
①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；
②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．
（1）求证：AF=DC ；
（2）若∠BAC=
，试判断四边形ADCF的形状，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（3分）如图，在直角坐标系中，直线
与坐标轴交于A、B两点，与双曲线
（
）交于点C，过点C作CD⊥x轴，垂足为D，且OA=AD，则以下结论：
①
；
②当0＜x＜3时，
；
③如图，当x=3时，EF=
；
④当x＞0时，
随x的增大而增大，
随x的增大而减小．
其中正确结论的个数是（ ）
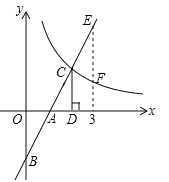
A．1 B．2 C．3 D．4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com