练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】夫子庙派出所巡警骑摩托车在东西大道上巡逻，某天他从岗亭出发，晚上停留在处，规定向东方向为正，当天行驶记录如下（单位：千米）：，，，，，，.

    （1）该巡警巡逻时离岗亭最远是多少千米.

    （2）若摩托车每行千米耗油升，那么该摩托车这天巡逻共耗油多少升？

    【答案】（1）最远是11千米；（2）3.96升

    【解析】

    （1）求出各个位置离出发点的距离，比较即可；

    （2）求出各数据绝对值之和，乘以0.05即可得到结果．

    解：（1）∵+11千米，11-9=2千米，2+7=9千米，9-14=-5千米，-5+8=3千米，3-13=-10千米，-10+4=-6千米，

    ∴每次离开出发点的距离是：+11千米， 2千米， 9千米，5千米， 3千米， 10千米， 6千米，

    ∴最远是11千米；

    （2）该巡警巡逻时，共行驶了11+9+7+14+8+13+4=66千米，

    若摩托车每行1千米耗油0.06升，那么该摩托车这天巡逻共耗油66×0.06=3.96升．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】生活与数学

    日

    一

    二

    三

    四

    五

    六

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    26

    27

    （1）姆同学在某月的日历上圈出2×2个数，正方形的方框内的四个数的和是48，那么这四个数是_______.

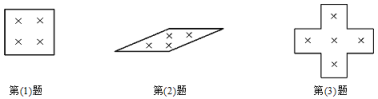
    （2）丽也在上面的日历上圈出2×2个数，斜框内的四个数的和是46，则它们分别是_____.

    （3）莉也在日历上圈出5个数，呈十字框形，它们的和是55，则中间的数是______.

    （4）某月有5个星期日的和是75，则这个月中最后一个星期日是______号？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（阅读理解）

    点A、B、C为数轴上三点，如果点C在A、B之间且到A的距离是点C到B的距离3倍，那么我们就称点C是{A，B}的奇点．

    例如，如图1，点A表示的数为﹣3，点B表示的数为1．表示0的点C到点A的距离是3，到点B的距离是1，那么点C是{A，B}的奇点；又如，表示﹣2的点D到点A的距离是1，到点B的距离是3，那么点D就不是{A，B}的奇点，但点D是{B，A}的奇点．

    （知识运用）

    如图2，M、N为数轴上两点，点M所表示的数为﹣3，点N所表示的数为5．

    （1）数　　　　 所表示的点是{M，N}的奇点；数　　　　 所表示的点是{N，M}的奇点；

    （2）如图3，A、B为数轴上两点，点A所表示的数为﹣50，点B所表示的数为30．现有一动点P从点B出发向左运动，当P点运动到数轴上的什么位置时，P、A和B中恰有一个点为其余两点的奇点？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

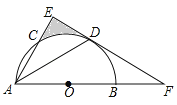
    【题目】如图，AB为半圆O的直径，AC是⊙O的一条弦，D为的中点，作DE⊥AC，交AB的延长线于点F，连接DA．

    （1）求证：EF为半圆O的切线；

    （2）若DA=DF=，求阴影区域的面积．（结果保留根号和π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)15－[3－(－5－4)]；

    (2)2.5－(－2)÷－1.5；

    (3)2－{8＋(－1)－[(－4)×2÷(－2)＋6×(－6)]}．

    (4)(－5)×(＋2019)＋(＋7)×(－2019)＋12×2019.

    (5) (用简便方法)．

    (6).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某超市销售一种牛奶，进价为每箱24元，规定售价不低于进价．现在的售价为每箱36元，每月可销售60箱．市场调查发现：若这种牛奶的售价每降价1元，则每月的销量将增加10箱，设每箱牛奶降价x元(x为正整数)，每月的销量为y箱．

    （1）写出y与x中间的函数关系式和自变量的取值范围；

    （2）超市如何定价，才能使每月销售牛奶的利润最大？最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC的顶点坐标分别为A（-2,1），B（-3,-2），C（1，-2）.把△ABC向上平移4个单位长度，再向右平移3个单位长度，得到△A′B′C′．

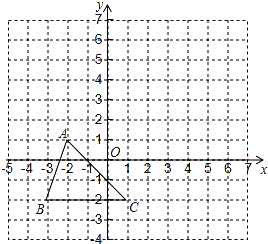
    （1）在图中画出△A′B′C′，并写出点A′，B′，C′的坐标；

    （2）连接A′C和A′A，求三角形AA′C的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：

    在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗？

    小敏在思考问题时，有如下思路：连接AC．

    结合小敏的思路作答：

    （1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由，参考小敏思考问题的方法解决一下问题；

    （2）如图2，在（1）的条件下，若连接AC，BD．

    ①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；

    ②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数轴上点对应的数分别是、，为数轴上两个动点，它们同时向右运动.点从点出发，速度为每秒个单位长度；点从点出发，速度为点的倍，点为原点.

    （1）当运动秒时，点对应的数分别是 、 .

    （2）求运动多少秒时，点中恰有一个点为另外两个点所连线段的中点？

    查看答案和解析>>

    同步练习册答案