Question

【题目】如图，抛物线y=ax2﹣5ax﹣4交x轴于A，B两点（点A位于点B的左侧），交y轴于点C，过点C作CD∥AB，交抛物线于点D，连接AC、AD，AD交y轴于点E，且AC=CD，过点A作射线AF交y轴于点F，AB平分∠EAF．

（1）此抛物线的对称轴是　 　；

（2）求该抛物线的解析式；

（3）若点P是抛物线位于第四象限图象上一动点，求△APF面积S△APF的最大值，以及此时点P的坐标；

（4）点M是线段AB上一点（不与点A，B重合），点N是线段AD上一点（不与点A，D重合），则两线段长度之和：MN+MD的最小值是　 　．

Answer 1

【答案】（1）直线x=；（2）抛物线解析式为y=x2﹣x﹣4；（3）当x=4时，S△APF的最大值为，此时P点坐标为（4，﹣）；（4）.

【解析】分析：(1)直接利用抛物线的对称轴方程求解;(2)先确定C(0,4)再利用对称性得到D(5,-4),从而得到CD=AC=5,然后求出A点的坐标，再把A点坐标代入y=ax-5ax-4中求出a即可;(3)作PQ∥y轴交AF于Q，如图1,先利用待定系数法确定直线AD的解析式为y=﹣x﹣得到E(0,-)，再根据等腰三角形的三线合一确定F（0,），则易得直线AF的解析式为y=，设P（x，-4）（0＜x＜8＝，则Q（x，） ，所以PQ= ，然后利用三角形面积公式，根据可表示出，最后利用二次函数的性质解决问题；
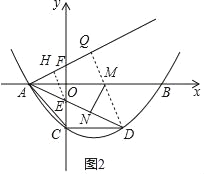
（4）作DQ⊥AF于Q，交x轴于M，作MN⊥AD于N，EH⊥AF于H，如图2，利用两点之间线段最短和垂线段最短判断此时MN+MD的值最小，再利用面积法求出EH，然后利用平行线分线段成比例定理计算DQ即可．

详解：（1）抛物线的对称轴为直线x=﹣=；

（2）当x=0时，y=ax2﹣5ax﹣4=﹣4，则C（0，﹣4）；

∵CD∥x轴，

∴点C与点D关于直线x=对称，

∴D（5，﹣4），CD=5，

∵AC=CD，

∴AC=5，

在Rt△AOC中，OA==3，

∴A（﹣3，0），

把A（﹣3，0）代入y=ax2﹣5ax﹣4得9a+15a﹣4=0，解得a=，

∴抛物线解析式为y=x2﹣x﹣4；

（3）作PQ∥y轴交AF于Q，如图1，

当y=0时， x2﹣x﹣4=0，解得x1=﹣3，x2=8，则P（8，0），

设直线AD的解析式为y=kx+b，

把A（﹣3，0），D（5，﹣4）代入得，解得，

∴直线AD的解析式为y=﹣x﹣，

当x=0时，y=﹣x﹣=﹣，则E（0，﹣），

∵AB平分∠EAF，AO⊥EF，

∴OF=OE=，

∴F（0，），

易得直线AF的解析式为y=x+，

设P（x， x2﹣x﹣4）（0＜x＜8），则Q（x， x+），

∴PQ=x+﹣（x2﹣x﹣4）=﹣x2+x+，

∴S△APF=S△PAQ﹣S△PFQ=3PQ=﹣x2+2x+=﹣（x﹣4）2+，

当x=4时，S△APF的最大值为，此时P点坐标为（4，﹣）；

（4）作DQ⊥AF于Q，交x轴于M，作MN⊥AD于N，EH⊥AF于H，如图2，

∵AB平分∠EAF，

∴MQ=MN，

∴MN+MD=DQ，

∴此时MN+MD的值最小，

∵A（﹣3，0），E（0，﹣），D（5，﹣4），

∴AE==，AD==4，

∵OAEF=EHAF，

∴EH==，

∵EH∥DQ，

∴=，即=，

∴DQ=，

即MN+MD的最小值是．

故答案为直线x=；．