
【题目】如图,将函数![]() 的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )
的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】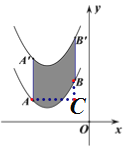
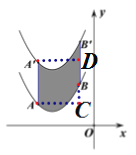
分析:过A作AC∥x轴,交B′B的延长线于点C,过A′作A′D∥x轴,交B′B的于点D,则C(-1,m),AC=-1-(-4)=3,根据平移的性质以及曲线段AB扫过的面积为9(图中的阴影部分),得出AA′=3,然后根据平移规律即可求解.
详解:过A作AC∥x轴,交B′B的延长线于点C,过A′作A′D∥x轴,交B′B的于点D,则C(-1,m),
∴AC=-1-(-4)=3,
∵曲线段AB扫过的面积为9(图中的阴影部分),
∴矩形ACD A′的面积等于9,
∴AC·AA′=3AA′=9,
∴AA′=3,
∴新函数的图是将函数y=![]() (x-2)2+1的图象沿y轴向上平移3个单位长度得到的,
(x-2)2+1的图象沿y轴向上平移3个单位长度得到的,
∴新图象的函数表达式是y=![]() (x-2)2+1+3=
(x-2)2+1+3=![]() (x-2)2+4.
(x-2)2+4.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH.
(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);
(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),
①试用含α的代数式表示∠HAE;
②求证:HE=HG;
③四边形EFGH是什么四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作平行四边形![]() ,使
,使![]() ,
,![]() ,”的作图过程.
,”的作图过程.
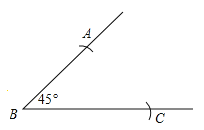
作法:如图,①作![]() ;
;
②在![]() 的两边上分别截取
的两边上分别截取![]() ,
,![]() ;
;
③以点![]() 为圆心,
为圆心,![]() 长为半径画弧,以点
长为半径画弧,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,两弧相交于点
长为半径画弧,两弧相交于点![]() ;
;
④连接![]() ,
,![]() .
.
则四边形![]() 为所求作的平行四边形.
为所求作的平行四边形.
根据小东设计的作图过程:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明: ![]()
![]() ______,
______,![]() ______,
______,
![]() 四边形
四边形![]() 是平行四边形.(______)(填推理的依据).
是平行四边形.(______)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为大半圆的直径,小半圆的圆心O1在线段CD上,大半圆O的弦AB与小半圆O1交于E、F,AB=6cm,EF=2cm,且AB∥CD。则阴影部分的面积为__________cm2(结果保留准确数)
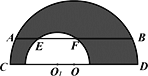
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题:
(1)求扇形统计图中m的值,并补全条形统计图;
(2)在被调查的学生中,随机抽一人,抽到选“体育特长类”或“艺术特长类”的学生的概率是多少?

(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
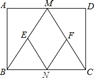
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)填空:当AB:AD= 时,四边形MENF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n是实数,定义运算“*”为:m*n=mn+n.
(1)分别求4*(﹣2)与4*![]() 的值;
的值;
(2)若关于x的方程x*(a*x)=﹣![]() 有两个相等的实数根,求实数a的值.
有两个相等的实数根,求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com