练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在四边形ABCD中，AB：BC：CD：DA=2：2：3：1，且∠ABC=90°，则∠DAB的度数是______°．

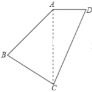
    【答案】135°

    【解析】

    由已知可得AB=BC，从而可求得∠BAC的度数.设AB＝2x ，通过计算证明AC2+AD2=CD2，从而证得ΔACD是直角三角形，即可得到∠DAC=90°，从而求得∠DAB的度数．

    解：∵AB：BC：CD：DA=2：2：3：1，且∠ABC=90°，
    ∴AB=BC，
    ∴∠BAC=∠ACB=45°，
    ∴设AB＝2x，则BC＝2x，CD=3x，DA=x,
    ∴AC2=AB2+BC2=(2x)2+(2x)2=8x2

    又CD2-AD2=(3x)2-x2=8x2

    ∴AC2= CD2-AD2

    ∵AC2+AD2=CD2
    ∴ΔACD是直角三角形，

    ∴∠DAC=90°，
    ∴∠DAB=45°+90°=135°．

    故答案是：135°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

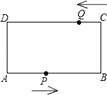
    【题目】如图，在矩形ABCD中，AB=24厘米，BC=10厘米，点P从A开始沿AB边以4厘米/秒的速度运动，点Q从C开始沿CD边2厘米/秒的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达终点时，另一点也随之停止运动，设运动时间为t秒．

    （1）当t=2秒时，求P、Q两点之间的距离；

    （2）t为何值时，线段AQ与DP互相平分？

    （3）t为何值时，四边形APQD的面积为矩形面积的？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直角三角形ABC中，∠C＝90°，将△ABC绕点A逆时针旋转至△AED，使点C的对应点D恰好落在边AB上，E为点B的对应点．设∠BAC＝α，则∠BED＝______.（用含α的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC中，∠B=90°，AB=16cm，BC=12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．

    （1）出发2秒后，求PQ的长.

    （2）当点Q在边BC上运动时，出发几秒钟后，△PQB能形成等腰三角形？

    （3）当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现在正是草莓热销的季节，某水果零售商店分两批次从批发市场共购进草莓40箱，已知第一、二次进货价分别为每箱50元、40元，且第二次比第一次多付款700元．

    （1）设第一、二次购进草莓的箱数分别为a箱、b箱，求a，b的值；

    （2）若商店对这40箱草莓先按每箱60元销售了x箱，其余的按每箱35元全部售完．

    ①求商店销售完全部草莓所获利润y（元）与x（箱）之间的函数关系式；

    ②当x的值至少为多少时，商店才不会亏本．（注：按整箱出售，利润＝销售总收入－进货总成本）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上点A所表示的数是，点B在点A的右侧，AB=6；点C在AB之间， AC=2BC．

    （1）在数轴上描出点B；

    （2）求点C所表示的数，并在数轴上描出点C；

    （3）已知在数轴上存在点P，使PA+PC=PB，求点P所表示的数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“分组合作学习”已成为推动课堂教学改革，打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析，统计图如下：

    请结合图中信息解答下列问题：

    （1）求出随机抽取调查的学生人数；

    （2）补全分组后学生学习兴趣的条形统计图；

    （3）分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

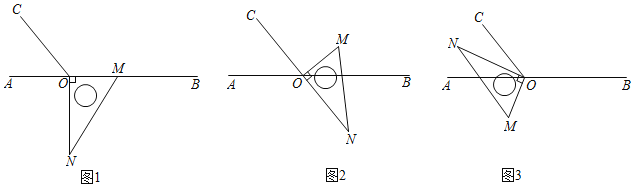
    【题目】如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC＝2∠AOC，将一直角三角板的直角顶点放在点O处，边OM在射线OB上，另一边ON在直线AB的下方．

    （1）将图1中的三角板绕点O按逆时针方向旋转45°至图2的位置，此时∠MOC＝　 　°；

    （2）将图1中的三角板绕点O按逆时针方向旋转至图3的位置，使得ON在∠AOC的内部．试探究∠AOM与∠NOC之间满足什么等量关系，并说明理由；

    （3）在上述直角三角板从图1逆时针旋转一周的过程中，若三角板绕点O按5°每秒的速度旋转，当直角三角板的直角边ON所在直线恰好平分∠AOC时，求此时三角板绕点O的运动时间t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将函数的图象沿y轴向上平移得到一条新函数的图象，其中点A（-4，m），B（-1，n）,平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是 （ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案