
【题目】如图,在数轴上点A所表示的数是![]() ,点B在点A的右侧,AB=6;点C在AB之间, AC=2BC.
,点B在点A的右侧,AB=6;点C在AB之间, AC=2BC.
(1)在数轴上描出点B;
(2)求点C所表示的数,并在数轴上描出点C;
(3)已知在数轴上存在点P,使PA+PC=PB,求点P所表示的数.
![]()
【答案】(1)见解析;(2)-1,图见解析;(3)-3或-7.
【解析】
(1)根据点A和AB之间的距离即可找到点B的位置;
(2)解法一:根据AC=2BC和AB=6求出B、C之间的距离,再利用点B的位置即可得出点C所表示的数;
解法二:利用方程的思想,将BC设为x,通过AB=6建立一个关于x的方程并解方程,再利用点B的位置即可得出点C所表示的数;
解法三:设点C所表示的数为x,将AC,BC表示出来,建立方程求解即可;
(3)解法一:因为PA+PC=PB,分①当点P在AC之间时,②当点P在点A左侧时两种情况分情进行讨论即可;
解法二:利用PA =PB-PC=BC=2直接找到A,P之间的距离即可得出答案.
解:(1)点B在数轴上的位置如图1所示.
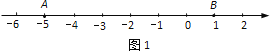
(2)解法一:因为AC=2BC,点C在AB之间,
所以AB=AC+BC=3BC.
因为AB=1-(-5)=6,
所以BC=2.
因为点B所表示的数是1,
1-2=-1
所以点C所表示的数是-1.
解法二:设BC=x,则AC=2x.
因为AB=1-(-5)=6,
所以x+2x=6.
解得x=2.
因为点B所表示的数是1,
1-2=-1
所以点C所表示的数是-1.
解法三:设点C所表示的数为x.
因为点C在AB之间,
所以BC=1-x,AC=x-(-5)= x +5.
因为AC=2BC,
所以x +5=2(1-x).
解得x=-1
点C在数轴上的位置如图2所示.
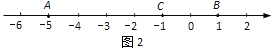
(3)解法一:因为PA+PC=PB,
所以点P在点C左侧.
因为点A表示的数是-5,点B表示的数是1,点C表示的数是-1,
所以AC =-1-(-5)=4,AB=1-(-5)=6.
①当点P在AC之间时,
设PA=x,则PC = AC- PA =4-x.
所以PB=PC+ BC =4-x +2=6-x.
因为PA+PC=PB,
所以x+4-x=6-x.
解得 x=2.
因为点A所表示的数是-5,-5+2=-3,
此时点P所表示的数是-3.
②当点P在点A左侧时,
设PA=x,则PC = PA+ AC =4+x,PB=PA+ AB =x +6,
因为PA+PC=PB,
所以x+4+x=6+x.
解得 x=2.
因为点A所表示的数是-5,-5-2=-7,
此时点P所表示的数是-7.
所以点P所表示的数是-3或-7.
解法二:因为PA+PC=PB,
所以点P在点C左侧.
所以PA =PB-PC=BC=2.
因为点A所表示的数是-5,
所以点P所表示的数是-3或-7.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(-4,0)、B(2,0),点C在y轴的正半轴上,且三角形ABC的面积为![]() .
.
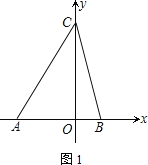
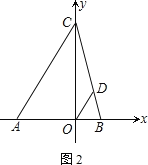
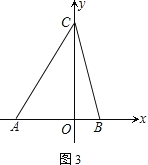
(1)求点C的坐标.
(2)过O点作OD平行于AC交CB于点D,问:x轴上是否存在一点P,使S△PBD=![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.
(3)若∠ACO=30°,射线CA绕C点以每秒3°的速度逆时针旋转到CA′,射线OB绕O点以每秒10°的速度逆时针旋转到OB′.当OB转动一周时两者都停止运动.若两射线同时开始运动,在旋转过程中,经过多长时间,CA′∥OB′?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,点D关于AB,AC的对称点分别是点E,F,四边形AEGF是平行四边形,则四边形AEGF面积的最小值是 ( )

A. 1B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O是正五边形ABCDE的中心,OA=1.
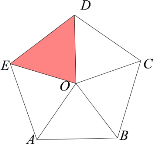
(1)△ODE绕着点 按 方向旋转 度,可以得到△OBC;
(2) △ODE沿 所在直线翻折,可以得到三角形 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格(边长为1的小正方形组成的网格纸,正方形的顶点称为格点)是我们在初中阶段常用的工具,利用它可以解决很多问题.
(1)如图①中,△ABC是格点三角形(三个顶点为格点),则它的面积为 ;
(2)如图②,在4×4网格中作出以A为顶点,且面积最大的格点正方形(四个顶点均为格点);
(3)人们发现,记格点多边形(顶点均为格点)内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为S=ma+nb-1,其中m,n为常数.试确定m,n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
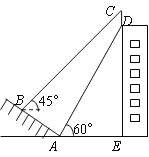
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有四个点A,B,C,D.
(1)根据下列语句画图:
①画射线BA;连接BD;
②画直线AD、BC相交于点E;
③在线段DC的延长线上取一点F,使CF=BC,连接EF;
(2)点B与直线AD的关系是 ;
(3)图中以E为顶点的角中,小于平角的角共有 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为大半圆的直径,小半圆的圆心O1在线段CD上,大半圆O的弦AB与小半圆O1交于E、F,AB=6cm,EF=2cm,且AB∥CD。则阴影部分的面积为__________cm2(结果保留准确数)
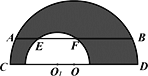
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com