
【题目】如图O是正五边形ABCDE的中心,OA=1.
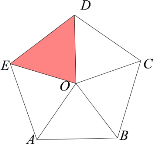
(1)△ODE绕着点 按 方向旋转 度,可以得到△OBC;
(2) △ODE沿 所在直线翻折,可以得到三角形 .
【答案】(1)O,顺时针,144;(或逆时针 216);(2) OD,△ODC.(或OC,△OAB)
【解析】
(1)先计算出正五边形的每各内角的度数,然后找到旋转中心,按照顺时针或逆时针找到一条对应边,看对应边的夹角是多少即可.
(2)根据翻折的性质,图形沿某条直线翻折,翻折后与翻折前图形能够完全重合,依次解决即可.
解:(1)正五边形的每各内角为360÷5=72,即72度,分两种情况讨论:
①△ODE绕着点O按顺时针方向旋转144度,即OE与OC重合,OD与OB,旋转角为∠DOB或∠EOC,可以得到△OBC;
②△ODE绕着点O按逆时针方向旋转216度,即OE与OC重合,OD与OB,可以得到△OBC;
(2)根据翻折的性质,翻折前后图形能够完全重合,即成轴对称,那条直线即为对称轴,可分两种情况:①故△ODE沿OD所在直线翻折,可以得到三角形ODC.
②故△ODE沿OC所在直线翻折,可以得到三角形OAB.


科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣6,点B表示8,点C表示16,我们称点A和点C在数轴上相距22个长度单位.动点P从点A出发,以1单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速:同时,动点Q从点C出发,以2单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
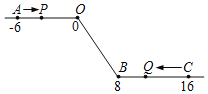
(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
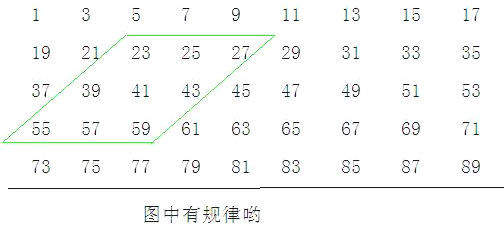
【题目】下图的数阵是由全体奇数排成:
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在数阵图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由;
(3)这九个数之和能等于1998吗?2005,1017呢?若能,请写出这九个数中最小的一个;若不能,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长.
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ∥
∥![]() ,BE∥CF,BA⊥
,BE∥CF,BA⊥![]() ,DC⊥
,DC⊥![]() ,下面给出四个结论:①BE=CF;②AB=DC;③
,下面给出四个结论:①BE=CF;②AB=DC;③![]() ;
;
④四边形ABCD是矩形.其中说法正确的有( )
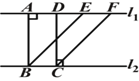
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A所表示的数是![]() ,点B在点A的右侧,AB=6;点C在AB之间, AC=2BC.
,点B在点A的右侧,AB=6;点C在AB之间, AC=2BC.
(1)在数轴上描出点B;
(2)求点C所表示的数,并在数轴上描出点C;
(3)已知在数轴上存在点P,使PA+PC=PB,求点P所表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某一城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天,乙队单独完成这项工程需要90天;若由甲队先做20天,剩下的工程由甲、乙两队合做完成.
(1)甲、乙两队合作多少天?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com