
【题目】若直线![]() 经过点
经过点![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 与
与![]() 关于
关于![]() 轴对称,则
轴对称,则![]() 与
与![]() 的交点坐标为( )
的交点坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据![]() 与
与![]() 关于x轴对称,可知
关于x轴对称,可知![]() 必经过(0,-4),
必经过(0,-4),![]() 必经过点(3,-2),然后根据待定系数法分别求出
必经过点(3,-2),然后根据待定系数法分别求出![]() 、
、![]() 的解析式后,再联立解方程组即可求得
的解析式后,再联立解方程组即可求得![]() 与
与![]() 的交点坐标.
的交点坐标.
∵直线![]() 经过点(0,4),
经过点(0,4),![]() 经过点(3,2),且
经过点(3,2),且![]() 与
与![]() 关于x轴对称,
关于x轴对称,
∴直线![]() 经过点(3,﹣2),
经过点(3,﹣2),![]() 经过点(0,﹣4),
经过点(0,﹣4),
设直线![]() 的解析式y=kx+b,
的解析式y=kx+b,
把(0,4)和(3,﹣2)代入直线![]() 的解析式y=kx+b,
的解析式y=kx+b,
则![]() ,
,
解得:![]() ,
,
故直线![]() 的解析式为:y=﹣2x+4,
的解析式为:y=﹣2x+4,
设l2的解析式为y=mx+n,
把(0,﹣4)和(3,2)代入直线![]() 的解析式y=mx+n,
的解析式y=mx+n,
则![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为:y=2x﹣4,
的解析式为:y=2x﹣4,
联立![]() ,解得:
,解得:![]()
即![]() 与
与![]() 的交点坐标为(2,0).
的交点坐标为(2,0).
故选D.


科目:初中数学 来源: 题型:
【题目】如图,已知函数y-![]() xb的图象与x轴、y轴分别交于点A、B,与函数yx的图象交于点M,点M的横坐标为2,在x轴上有一点Pa,0(其中a2),过点P作x轴的垂线,分别交函数y
xb的图象与x轴、y轴分别交于点A、B,与函数yx的图象交于点M,点M的横坐标为2,在x轴上有一点Pa,0(其中a2),过点P作x轴的垂线,分别交函数y![]() xb和yx的图象于点C、D.
xb和yx的图象于点C、D.
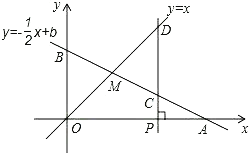
(1)求点M的坐标;
(2)求点A的坐标;
(3)若OBCD,求a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O是正五边形ABCDE的中心,OA=1.
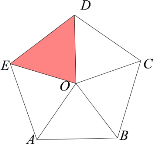
(1)△ODE绕着点 按 方向旋转 度,可以得到△OBC;
(2) △ODE沿 所在直线翻折,可以得到三角形 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格(边长为1的小正方形组成的网格纸,正方形的顶点称为格点)是我们在初中阶段常用的工具,利用它可以解决很多问题.
(1)如图①中,△ABC是格点三角形(三个顶点为格点),则它的面积为 ;
(2)如图②,在4×4网格中作出以A为顶点,且面积最大的格点正方形(四个顶点均为格点);
(3)人们发现,记格点多边形(顶点均为格点)内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为S=ma+nb-1,其中m,n为常数.试确定m,n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
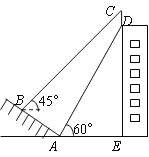
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=![]() ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有四个点A,B,C,D.
(1)根据下列语句画图:
①画射线BA;连接BD;
②画直线AD、BC相交于点E;
③在线段DC的延长线上取一点F,使CF=BC,连接EF;
(2)点B与直线AD的关系是 ;
(3)图中以E为顶点的角中,小于平角的角共有 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一只纸箱中装有除颜色外完全相同的红色、黄色、蓝色乒乓球共100个.从纸箱中任意摸出一球,摸到红色球、黄色球的概率分别是0.2、0.3.
(1)试求出纸箱中蓝色球的个数;
(2)小明向纸箱中再放进红色球若干个,小丽为了估计放入的红球的个数,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到红球的频率在0.5附近波动,请据此估计小明放入的红球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳某工厂从美国进口A、B两种产品销售,已知每台A种产品进价为3000元,售价为4800元;受中美贸易大战的影响,每台B种产品的进价上涨500元,进口相同数量的B种产品,在中美贸易大战开始之前只需要60万元,中美贸易大战开始之后需要80万元。
(1)中美贸易大战开始之后,每台B种产品的进价为多少?
(2)中美贸易大战开始之后,如果A种产品的进价和售价不变,每台B种产品在进价的基础上提高40%作为售价。公司筹集到不多于35万元且不少于33万元的资金用于进口A、B两种产品共150台,请你设计一种进货方案使销售后的总利润最大。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com