
【题目】如图,已知函数y-![]() xb的图象与x轴、y轴分别交于点A、B,与函数yx的图象交于点M,点M的横坐标为2,在x轴上有一点Pa,0(其中a2),过点P作x轴的垂线,分别交函数y
xb的图象与x轴、y轴分别交于点A、B,与函数yx的图象交于点M,点M的横坐标为2,在x轴上有一点Pa,0(其中a2),过点P作x轴的垂线,分别交函数y![]() xb和yx的图象于点C、D.
xb和yx的图象于点C、D.
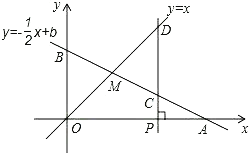
(1)求点M的坐标;
(2)求点A的坐标;
(3)若OBCD,求a的值。
【答案】(1)(2,2);(2)(6,0);(3)a=4.
【解析】
(1)将x=2代入y=x中求出y值,由此即可得出点M的坐标;
(2)根据点M的坐标利用待定系数法即可求出一次函数解析式,再将y=0代入一次函数解析式中求出x值,由此即可得出点A的坐标;
(3)将x=0代入一次函数解析式求出y值,由此即可得出点B的坐标,进而可得出CD=OB=3,再根据一次函数解析式上点的坐标特征即可得出点C、D的坐标,利用两点间的距离公式即可得出关于a的一元一次方程,解之即可得出结论.
解:(1)∵点M在直线y=x的图象上,且点M的横坐标为2,
∴y=x=2,
∴点M的坐标为(2,2).
(2)把M(2,2)代入y=-![]() x+b得:-1+b=2,
x+b得:-1+b=2,
解得:b=3,
∴一次函数的解析式为y=-![]() x+3.
x+3.
当y=-![]() x+3=0时,x=6,
x+3=0时,x=6,
∴A点坐标为(6,0).
(3)当x=0时,y=-![]() x+3=3,
x+3=3,
∴点B的坐标为(0,3),
∴OB=3.
∵CD=OB,
∴CD=3.
∵PC⊥x轴,
∴点C的坐标为(a,-![]() a+3),点D的坐标为(a,a),
a+3),点D的坐标为(a,a),
∴CD=a-(-![]() a+3)=3,
a+3)=3,
∴a=4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
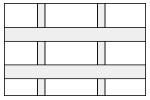
【题目】如图,某小区规划在一个长30 m,宽20 m的矩形场地上修建两横竖通道,横竖通道的宽度比为2∶1,其余部分种植花草,若通道所占面积是整个场地面积 的![]() .
.
(1)求横、竖通道的宽各为多少?
(2)若修建1 m2道路需投资750元,种植1 m2花草需投资250元,此次修建需投资多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过点A0,2的直线l1:y1kxbk0与直线l2:y2x1交于点P2,m。
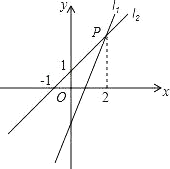
(1)求点P的坐标和直线l1的解析式;
(2)直接写出使得y1y2的x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
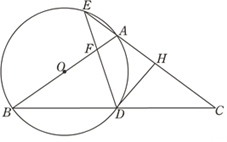
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若![]() ,求证:A为EH的中点.
,求证:A为EH的中点.
(3)若EA=EF=1,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点Pa,b和点Qa,b,给出如下定义:若![]() ,则称点Q为点P的限变点,例如:点(2,3)的限变点的坐标是(2,3),点2,5的限变点的坐标是2,5。
,则称点Q为点P的限变点,例如:点(2,3)的限变点的坐标是(2,3),点2,5的限变点的坐标是2,5。
(1)在点A2,1,B1,2中有一个点是函数y=![]() 图象上某一个点的限变点,这个点是 ;
图象上某一个点的限变点,这个点是 ;
(2)求点![]() ,1的限变点的坐标;
,1的限变点的坐标;
(3)若点P在函数yx32xk,k2的图象上,其限变点Q的纵坐标b的取值范围是5b2,求k的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
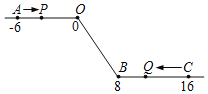
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣6,点B表示8,点C表示16,我们称点A和点C在数轴上相距22个长度单位.动点P从点A出发,以1单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速:同时,动点Q从点C出发,以2单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
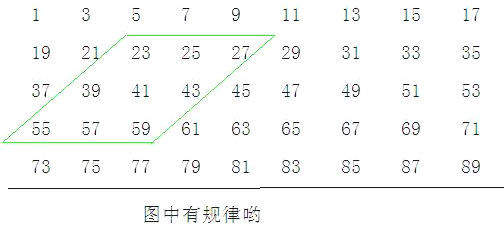
【题目】下图的数阵是由全体奇数排成:
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在数阵图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由;
(3)这九个数之和能等于1998吗?2005,1017呢?若能,请写出这九个数中最小的一个;若不能,请说出理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com