练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】过点A0,2的直线l1:y1kxbk0与直线l2:y2x1交于点P2,m。

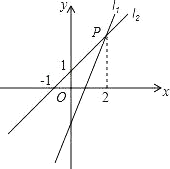
    （1）求点P的坐标和直线l1的解析式；

    （2）直接写出使得y1y2的x的取值范围。

    【答案】(1) y1=x-2;(2) x≤2．

    【解析】

    （1）由点P的横坐标利用一次函数图象上点的坐标特征即可求出点P的坐标，根据点A、P的坐标，利用待定系数法即可求出直线l1的解析式；
    （2）根据两函数图象的上下位置关系即可得出不等式的解集．

    解：（1）当x=2时，m=2+1=3，
    ∴点P（2，3）．
    将点A（0，-2）、P（2，3）代入y1=kx+b中，
    得：，解得：，
    ∴直线l1的解析式为y1=x-2．
    （2）观察两函数图象可知：
    当x＜2时，直线l1在直线l2的下方，
    ∴使得y1≤y2的x的取值范围为x≤2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】元旦放假时，小明一家三口一起乘小轿车去探望爷爷、奶奶和姥爷、姥姥．早上从家里出发，向东走了5千米到超市买东西，然后又向东走了2.5千米到爷爷家，下午从爷爷家出发向西走了10千米到姥爷家，晚上返回家里．

    （1）若以小明家为原点，向东为正方向，用1个单位长度表示1千米，请将超市、爷爷家和姥爷家的位置在下面数轴上分别用点A、B、C表示出来；

    （2）超市和姥爷家相距多少千米？

    （3）若小轿车每千米耗油0.08升，求小明一家从出发到返回家，小轿车的耗油量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人参加某体育项目训练，为了便于研究，把最后5次的训练成绩分别用实线和虚线连接起来，如图，下面的结论错误的是（　　）

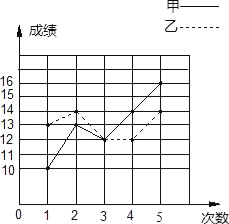
    A. 乙的第2次成绩与第5次成绩相同

    B. 第3次测试，甲的成绩与乙的成绩相同

    C. 第4次测试，甲的成绩比乙的成绩多2分

    D. 在5次测试中，甲的成绩都比乙的成绩高

    查看答案和解析>>

    科目：初中数学 来源： 题型：

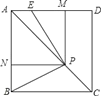
    【题目】如图，已知正方形ABCD的边长为1，P是对角线AC上任意一点，E为AD上的点，且∠EPB=90°，PM⊥AD，PN⊥AB．

    （1）求证：四边形PMAN是正方形；

    （2）求证：EM=BN；

    （3）若点P在线段AC上移动，其他不变，设PC=x，AE=y，求y关于x的解析式，并写出自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，A(－4，0)、B(2，0)，点C在y轴的正半轴上，且三角形ABC的面积为．

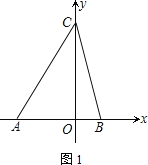
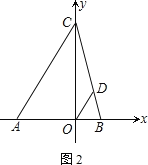
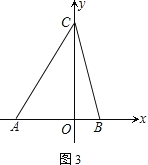
    （1）求点C的坐标．

    （2）过O点作OD平行于AC交CB于点D，问：x轴上是否存在一点P，使S△PBD＝？若存在，求出点P的坐标；若不存在，请说明理由．

    （3）若∠ACO＝30°，射线CA绕C点以每秒3°的速度逆时针旋转到CA′，射线OB绕O点以每秒10°的速度逆时针旋转到OB′．当OB转动一周时两者都停止运动．若两射线同时开始运动，在旋转过程中，经过多长时间，CA′∥OB′？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y1=ax2+2ax+1与轴有且仅有一个公共点A，经过点A的直线y2=kx+b交该抛物线于点B，交y轴于点C，且点C是线段AB的中点．

    (1)求的值；

    (2)求直线AB对应的函数解析式；

    (3)直接写出当y1 ≥y2 时，的取值范围．

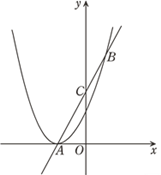
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知函数y-xb的图象与x轴、y轴分别交于点A、B，与函数yx的图象交于点M，点M的横坐标为2，在x轴上有一点Pa,0（其中a2），过点P作x轴的垂线，分别交函数yxb和yx的图象于点C、D.

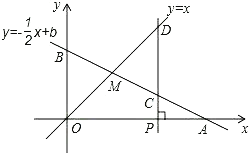
    （1）求点M的坐标；

    （2）求点A的坐标；

    （3）若OBCD，求a的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个四位数，记千位上和百位上的数字之和为，十位上和个位上的数字之和为，如果，那么称这个四位数为“和平数”.例如：1423，，，因为，所以1423是“和平数”.

    （1）直接写出：最小的“和平数”是_________________，最大的“和平数”是_______________；

    （2）求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正方形网格（边长为1的小正方形组成的网格纸，正方形的顶点称为格点）是我们在初中阶段常用的工具，利用它可以解决很多问题．

    （1）如图①中，△ABC是格点三角形（三个顶点为格点），则它的面积为 ；

    （2）如图②，在4×4网格中作出以A为顶点，且面积最大的格点正方形（四个顶点均为格点）；

    （3）人们发现，记格点多边形（顶点均为格点）内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为S＝ma＋nb－1，其中m，n为常数．试确定m，n的值．

    查看答案和解析>>

    同步练习册答案