
【题目】一个四位数,记千位上和百位上的数字之和为![]() ,十位上和个位上的数字之和为
,十位上和个位上的数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“和平数”.例如:1423,
,那么称这个四位数为“和平数”.例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是_________________,最大的“和平数”是_______________;
(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”.
【答案】(1)1001,9999;(2)2754和4848.
【解析】
(1)根据“和平数”的定义,即可得到结论;
(2)设这个“和平数”为1000a+100b+10c+d,于是得到d=2a,a+b=c+d,b+c=12k,求得2c+a=12k,即a=2、4,6,8;d=4、8、12(舍去)、16(舍去);①、当a=2,d=4时,2(c+1)=12k,得到c=5则b=7,②、当a=4,d=8时,得到c=4则b=8,于是得到结论;
解:(1)根据题意,最小的“和平数”为1001,最大的“和平数”为9999;
故答案为:1001,9999;
(2)设这个“和平数”为:1000a+100b+10c+d,
则d=2a,a+b=c+d,b+c=12k,k为整数,
∴2c+a=12k,
即a=2,4,6,8,12(舍去),16(舍去),
当a=2,d=4时,2(c+1)=12k,
可知:c+1=6k,且a+b=c+d,
∴c=5,b=7;
当a=4,d=8时,2(c+2)=12k,
可知:c+2=6k,且a+b=c+d,
∴c=4,b=8;
综上所述:这个数为:2754和4848.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是面积为4![]() 的等边三角形,△ABC∽△ADE,
的等边三角形,△ABC∽△ADE,
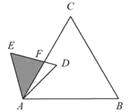
AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积
等于___(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过点A0,2的直线l1:y1kxbk0与直线l2:y2x1交于点P2,m。
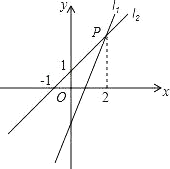
(1)求点P的坐标和直线l1的解析式;
(2)直接写出使得y1y2的x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点Pa,b和点Qa,b,给出如下定义:若![]() ,则称点Q为点P的限变点,例如:点(2,3)的限变点的坐标是(2,3),点2,5的限变点的坐标是2,5。
,则称点Q为点P的限变点,例如:点(2,3)的限变点的坐标是(2,3),点2,5的限变点的坐标是2,5。
(1)在点A2,1,B1,2中有一个点是函数y=![]() 图象上某一个点的限变点,这个点是 ;
图象上某一个点的限变点,这个点是 ;
(2)求点![]() ,1的限变点的坐标;
,1的限变点的坐标;
(3)若点P在函数yx32xk,k2的图象上,其限变点Q的纵坐标b的取值范围是5b2,求k的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣6,点B表示8,点C表示16,我们称点A和点C在数轴上相距22个长度单位.动点P从点A出发,以1单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速:同时,动点Q从点C出发,以2单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
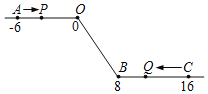
(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击队教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:

(1)根据上述信息可知:甲命中环数的中位数是 环,乙命中环数的众数是 环;
(2)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会 .(填 “变大”、“变小” 或 “不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
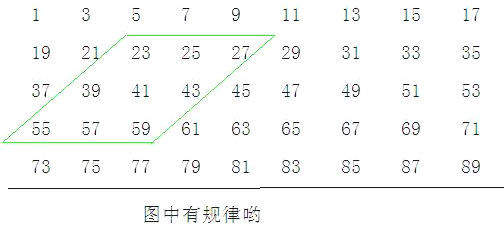
【题目】下图的数阵是由全体奇数排成:
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在数阵图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由;
(3)这九个数之和能等于1998吗?2005,1017呢?若能,请写出这九个数中最小的一个;若不能,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ∥
∥![]() ,BE∥CF,BA⊥
,BE∥CF,BA⊥![]() ,DC⊥
,DC⊥![]() ,下面给出四个结论:①BE=CF;②AB=DC;③
,下面给出四个结论:①BE=CF;②AB=DC;③![]() ;
;
④四边形ABCD是矩形.其中说法正确的有( )
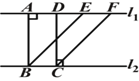
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知Rt△ABC中,∠C=90°,AC=4,BC=3,点A(6,5),B(2,8),反比例函数y![]() 过点C,过点A作AD∥y轴交双曲线于点D.
过点C,过点A作AD∥y轴交双曲线于点D.
(1)求反比例函数y![]() 的解析式;
的解析式;
(2)动点P在y轴正半轴运动,当线段PC与线段PD的差最大时,求P点的坐标;
(3)将Rt△ABC沿直线CO方向平移,使点C移动到点O,求线段AB扫过的面积.
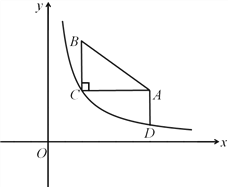
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com