
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ�����������ᡱ��ͼ�е�A��ʾ��6����B��ʾ8����C��ʾ16�����dzƵ�A�͵�C�����������22�����ȵ�λ������P�ӵ�A��������1��λ/����ٶ����š��������ᡱ���������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������Q�ӵ�C��������2��λ/����ٶ���������ĸ������˶����ӵ�B�˶�����O�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊt�룮
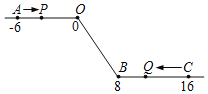
��1������P�ӵ�A�˶���C����Ҫ����ʱ�䣿
��2��P��Q��������ʱ�����������M����Ӧ�����Ƕ��٣�
��3����tΪ��ֵʱ��P��O���������������ij�����Q��B���������������ij�����ȣ�
���𰸡���1����P�ӵ�A�˶���C����Ҫ��ʱ����32�룻��2��������M����Ӧ������0����3��tΪ2s����4.4sʱ��P��O���������������ij�����Q��B���������������ij�����ȣ�
��������
��1������ʱ�䣽![]() ���ֶ����ÿ�������ϵ�ʱ������ͼ��ɣ�
���ֶ����ÿ�������ϵ�ʱ������ͼ��ɣ�
��2��P��Q��������ʱ������ʱ����ȣ����ݵ�����ϵ����һԪһ�η��̣�
��3������P��O���������������ij�����Q��B���������������ij�����ȿ����ж�ʱ����ȣ����ݵ�����ϵ����һԪһ�η��̣�ͬʱ��Ҫ��������ۣ�����ȻPO��OP����PO��OP����ͬһ���߶Σ�
�⣺��1����P�ӵ�A�˶���C����Ҫ��ʱ��
t��6��1+8��0.5+��16��8����1��32���룩
�𣺵�P�ӵ�A�˶���C����Ҫ��ʱ����32��
��2�������֪��P��Q�����������߶�OB����M������OM��x����
6��1+x��0.5��8��2+��8��x����4
���x��0
��OM��0��ʾP��Q�����������߶�OB����O������������M����Ӧ������0��
��3��P��O���������������ij�����Q��B���������������ij��������2�ֿ��ܣ�
������P��AO�ϣ�����Q��CB�ϣ�
��6��t��8��2t
��ã�t��2��
������P��AO�ϣ�����Q��BO�ϣ�
��6��t��4��t��4��
��ã�t��4.4
��tΪ2s����4.4sʱ��P��O���������������ij�����Q��B���������������ij�����ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������0.2m/s���ٶ���ƽ���ϰ���ͼ�еIJ������ߣ���ô�û����˴ӿ�ʼ��ֹͣ����ʱ��Ϊ__s��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A(��4��0)��B(2��0)����C��y����������ϣ���������ABC�����Ϊ![]() ��
��
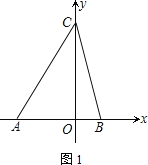
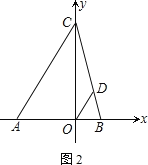
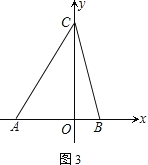
��1�����C�����꣮
��2����O����ODƽ����AC��CB�ڵ�D���ʣ�x�����Ƿ����һ��P��ʹS��PBD��![]() �������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��3������ACO��30��������CA��C����ÿ��3�����ٶ���ʱ����ת��CA��������OB��O����ÿ��10�����ٶ���ʱ����ת��OB������OBת��һ��ʱ���߶�ֹͣ�˶�����������ͬʱ��ʼ�˶�������ת�����У������ʱ�䣬CA����OB����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����y-![]() xb��ͼ����x�ᡢy��ֱ��ڵ�A��B���뺯��yx��ͼ���ڵ�M����M�ĺ�����Ϊ2����x������һ��Pa,0������a2��������P��x��Ĵ��ߣ��ֱ���y
xb��ͼ����x�ᡢy��ֱ��ڵ�A��B���뺯��yx��ͼ���ڵ�M����M�ĺ�����Ϊ2����x������һ��Pa,0������a2��������P��x��Ĵ��ߣ��ֱ���y![]() xb��yx��ͼ���ڵ�C��D.
xb��yx��ͼ���ڵ�C��D.
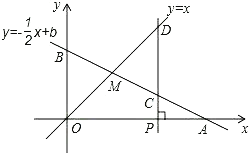
��1�����M�����ꣻ
��2�����A�����ꣻ
��3����OBCD����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ����ȫ�����������ǣ�2008���������������̻�����Ͷ����ʽ���2000��Ԫ��2010��Ͷ����ʽ���2420��Ԫ���Ҵ�2008�굽2010�꣬�����ÿ��Ͷ���ʽ����ƽ����������ͬ��
��1������ж������̻�����Ͷ���ʽ����ƽ�������ʣ�
��2����Ͷ���ʽ����ƽ�������ʲ��䣬��ô������2012����Ͷ�������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����λ������ǧλ�ϺͰ�λ�ϵ�����֮��Ϊ![]() ��ʮλ�Ϻ�λ�ϵ�����֮��Ϊ
��ʮλ�Ϻ�λ�ϵ�����֮��Ϊ![]() �����
�����![]() ����ô�������λ��Ϊ����ƽ����.���磺1423��
����ô�������λ��Ϊ����ƽ����.���磺1423��![]() ��
��![]() ����Ϊ
����Ϊ![]() ������1423�ǡ���ƽ����.
������1423�ǡ���ƽ����.
��1��ֱ��д������С�ġ���ƽ������_________________�����ġ���ƽ������_______________��
��2�����λ�ϵ�������ǧλ�ϵ����ֵ������Ұ�λ�ϵ�������ʮλ�ϵ�����֮����12�ı��������С���ƽ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���BAC��60������B��45����AB��2����D��BC�ϵ�һ�����㣬��D����AB��AC�ĶԳƵ�ֱ��ǵ�E��F���ı���AEGF��ƽ���ı��Σ����ı���AEGF�������Сֵ�� �� ��

A. 1B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼO���������ABCDE�����ģ�OA=1��
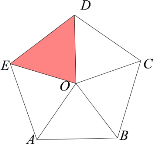
��1����ODE���ŵ� �� ������ת �ȣ����Եõ���OBC��
��2�� ��ODE�� ����ֱ�߷��ۣ����Եõ������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ�������ĸ���A��B��C��D��
��1������������仭ͼ��
�ٻ�����BA������BD��
�ڻ�ֱ��AD��BC�ཻ�ڵ�E��
�����߶�DC���ӳ�����ȡһ��F��ʹCF��BC������EF��
��2����B��ֱ��AD�Ĺ�ϵ���� ����
��3��ͼ����EΪ����Ľ��У�С��ƽ�ǵĽǹ����� ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com