练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某市为争创全国文明卫生城，2008年市政府对市区绿化工程投入的资金是2000万元，2010年投入的资金是2420万元，且从2008年到2010年，两年间每年投入资金的年平均增长率相同．

    （1）求该市对市区绿化工程投入资金的年平均增长率；

    （2）若投入资金的年平均增长率不变，那么该市在2012年需投入多少万元？

    【答案】（1）该市对市区绿化工程投入资金的年平均增长率为10%；（2）2012年需投入资金2928.2万元．

    【解析】分析:(1)因为年平均增长率相同，所以可设年平均增长率为，则;(2)需投入万元.

    解：（1）设该市对市区绿化工程投入资金的年平均增长率为，

    根据题意得，，

    解得，（舍去）.

    答：该市对市区绿化工程投入资金的年平均增长率为10﹪.

    （2）2012年需投入资金：（万元）.

    答：2012年需投入资金2 928.2万元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下图是昌平区2019年1月份每天的最低和最高气温，观察此图，下列说法正确的是（ ）

    A.在1月份中，最高气温为10℃，最低气温为－2℃

    B.在10号至16号的气温中，每天温差最小为7℃

    C.每天的最高气温均高于0℃，最低气温均低于0℃

    D.每天的最高气温与最低气温都是具有相反意义的量

    查看答案和解析>>

    科目：初中数学 来源： 题型：

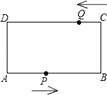
    【题目】如图，在矩形ABCD中，AB=24厘米，BC=10厘米，点P从A开始沿AB边以4厘米/秒的速度运动，点Q从C开始沿CD边2厘米/秒的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达终点时，另一点也随之停止运动，设运动时间为t秒．

    （1）当t=2秒时，求P、Q两点之间的距离；

    （2）t为何值时，线段AQ与DP互相平分？

    （3）t为何值时，四边形APQD的面积为矩形面积的？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

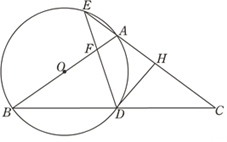
    【题目】如图，在△ABC中，AB=AC，以AB为直径作圆O，分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，连接DE交线段OA于点F．

    (1)求证：DH是圆O的切线；

    (2)若，求证：A为EH的中点．

    (3)若EA=EF=1，求圆O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在一张长方形纸条上画一条数轴．

    （1）若折叠纸条使数轴上表示﹣1的点与表示5的点重合，则折痕与数轴的交点表示的数是　 　；

    （2）如果数轴上两点之间的距离为6+m2（m为常数），这两点经过（1）的折叠方式后折痕与数轴的交点与（1）中的交点相同，求左边这个点表示的数；（用含m的代数式表示）

    （3）如图2，若将此纸条沿A，B处剪开，将中间的一段纸条对折，使其左右两端重合，这样连续对折n次后，再将其展开，求最右端的折痕与数轴的交点表示的数．（用含n的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”．图中点A表示﹣6，点B表示8，点C表示16，我们称点A和点C在数轴上相距22个长度单位．动点P从点A出发，以1单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速：同时，动点Q从点C出发，以2单位/秒的速度沿着数轴的负方向运动，从点B运动到点O期间速度变为原来的两倍，之后也立刻恢复原速．设运动的时间为t秒．

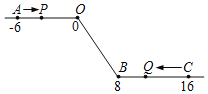
    （1）动点P从点A运动至C点需要多少时间？

    （2）P、Q两点相遇时，求出相遇点M所对应的数是多少；

    （3）求当t为何值时，P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直角三角形ABC中，∠C＝90°，将△ABC绕点A逆时针旋转至△AED，使点C的对应点D恰好落在边AB上，E为点B的对应点．设∠BAC＝α，则∠BED＝______.（用含α的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC中，∠B=90°，AB=16cm，BC=12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．

    （1）出发2秒后，求PQ的长.

    （2）当点Q在边BC上运动时，出发几秒钟后，△PQB能形成等腰三角形？

    （3）当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

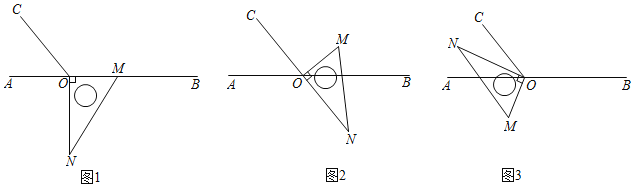
    【题目】如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC＝2∠AOC，将一直角三角板的直角顶点放在点O处，边OM在射线OB上，另一边ON在直线AB的下方．

    （1）将图1中的三角板绕点O按逆时针方向旋转45°至图2的位置，此时∠MOC＝　 　°；

    （2）将图1中的三角板绕点O按逆时针方向旋转至图3的位置，使得ON在∠AOC的内部．试探究∠AOM与∠NOC之间满足什么等量关系，并说明理由；

    （3）在上述直角三角板从图1逆时针旋转一周的过程中，若三角板绕点O按5°每秒的速度旋转，当直角三角板的直角边ON所在直线恰好平分∠AOC时，求此时三角板绕点O的运动时间t的值．

    查看答案和解析>>

    同步练习册答案