
【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长.
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形
;(3)当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形
【解析】
(1)根据点P、Q的运动速度求出AP,再求出BP和BQ,用勾股定理求得PQ即可;
(2)设出发t秒钟后,△PQB能形成等腰三角形,则BP=BQ,由BQ=2t,BP=8-t,列式求得t即可;
(3)当点Q在边CA上运动时,能使△BCQ成为等腰三角形的运动时间有三种情况:
①当CQ=BQ时,则∠C=∠CBQ,可证明∠A=∠ABQ,则BQ=AQ,则CQ=AQ,从而求得t;
②当CQ=BC时,则BC+CQ=12,易求得t;
③当BC=BQ时,过B点作BE⊥AC于点E,则求出BE,CE,即可得出t.
(1)∵BQ=2×2=4(cm),BP=ABAP=162×1=14(cm ),∠B=90°,
∴PQ=![]() =
=![]() (cm);
(cm);
(2)BQ=2t,BP=16t,
根据题意得:2t=16t,
解得:t=![]() ,
,
即出发![]() 秒钟后,△PQB能形成等腰三角形;
秒钟后,△PQB能形成等腰三角形;
(3)①当CQ=BQ时,如图1所示,
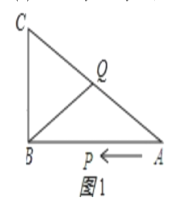
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°.
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ=10,
∴BC+CQ=22,
∴t=22÷2=11秒。
②当CQ=BC时,如图2所示,

则BC+CQ=24,
∴t=24÷2=12秒。
③当BC=BQ时,如图3所示,
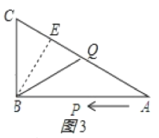
过B点作BE⊥AC于点E,
则BE=![]() ,
,
∴CE=![]() ,
,
∴CQ=2CE=14.4,
∴BC+CQ=26.4,
∴t=26.4÷2=13.2秒。
综上所述:当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形


科目:初中数学 来源: 题型:
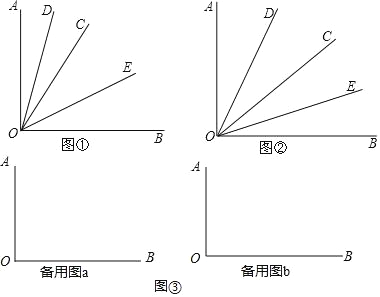
【题目】已知:∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,若射线OC在∠AOB内部绕O点旋转,当∠BOC=α时,求∠DOE的度数.
(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,直接写出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为争创全国文明卫生城,2008年市政府对市区绿化工程投入的资金是2000万元,2010年投入的资金是2420万元,且从2008年到2010年,两年间每年投入资金的年平均增长率相同.
(1)求该市对市区绿化工程投入资金的年平均增长率;
(2)若投入资金的年平均增长率不变,那么该市在2012年需投入多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,点D关于AB,AC的对称点分别是点E,F,四边形AEGF是平行四边形,则四边形AEGF面积的最小值是 ( )

A. 1B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
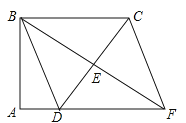
【题目】如图,在四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.
(1)求证:四边形BDFC是平行四边形;
(2)若CB=CD,求四边形BDFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O是正五边形ABCDE的中心,OA=1.
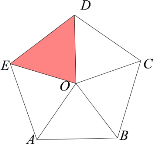
(1)△ODE绕着点 按 方向旋转 度,可以得到△OBC;
(2) △ODE沿 所在直线翻折,可以得到三角形 .
查看答案和解析>>
科目:初中数学 来源: 题型:
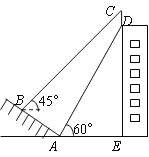
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH.
(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);
(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),
①试用含α的代数式表示∠HAE;
②求证:HE=HG;
③四边形EFGH是什么四边形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com