
【题目】已知:∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
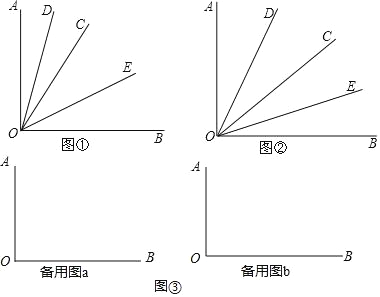
(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,若射线OC在∠AOB内部绕O点旋转,当∠BOC=α时,求∠DOE的度数.
(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,直接写出∠DOE的度数.
【答案】(1)45°;(2)45°;(3)45°或135°.
【解析】
(1)由∠BOC的度数求出∠AOC的度数,利用角平分线定义求出∠COD与∠COE的度数,相加即可求出∠DOE的度数;
(2)∠DOE度数不变,理由为:利用角平分线定义得到∠COD为∠AOC的一半,∠COE为∠COB的一半,而∠DOE=∠COD+∠COE,即可求出∠DOE度数为45度;
(3)分两种情况考虑,同理如图3,则∠DOE为45°;如图4,则∠DOE为135°.
(1)如图,∠AOC=90°﹣∠BOC=20°,
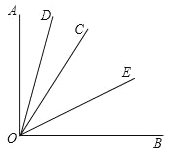
∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=∠AOC=10°,∠COE=![]() ∠BOC=35°,
∠BOC=35°,
∴∠DOE=∠COD+∠COE=45°;
(2)∠DOE的大小不变,理由是:
∠DOE=∠COD+∠COE=![]() ∠AOC+
∠AOC+![]() ∠COB=
∠COB=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)=![]() ∠AOB=45°;
∠AOB=45°;
(3)∠DOE的大小发生变化情况为:如图③,则∠DOE为45°;如图④,则∠DOE为135°,
分两种情况:如图3所示,
∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠DOE=∠COD﹣∠COE=![]() (∠AOC﹣∠BOC)=45°;
(∠AOC﹣∠BOC)=45°;
如图4所示,∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠DOE=∠COD+∠COE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ×270°=135°.
×270°=135°.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.

(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是昌平区2019年1月份每天的最低和最高气温,观察此图,下列说法正确的是( )

A.在1月份中,最高气温为10℃,最低气温为-2℃
B.在10号至16号的气温中,每天温差最小为7℃
C.每天的最高气温均高于0℃,最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,梯形ABCD中,AB//CD,且AB=2CD,E,F分别是AB,BC的中点.
EF与BD相交于点M.

(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,弧AB=弧AC,AP是⊙O的切线,交BO的延长线于点P
(1) 求证:AP∥BC
(2) 若tan∠P=![]() ,求tan∠PAC的值
,求tan∠PAC的值

查看答案和解析>>
科目:初中数学 来源: 题型:
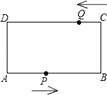
【题目】如图,在矩形ABCD中,AB=24厘米,BC=10厘米,点P从A开始沿AB边以4厘米/秒的速度运动,点Q从C开始沿CD边2厘米/秒的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒.
(1)当t=2秒时,求P、Q两点之间的距离;
(2)t为何值时,线段AQ与DP互相平分?
(3)t为何值时,四边形APQD的面积为矩形面积的![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
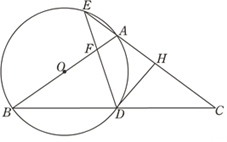
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若![]() ,求证:A为EH的中点.
,求证:A为EH的中点.
(3)若EA=EF=1,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长.
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com