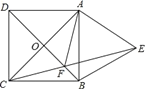
【题目】如图，已知正方形ABCD，以AB为边向外作等边三角形ABE，CE与DB相交于点F，则∠AFD的度数____．
【答案】60°
【解析】
根据正方形及等边三角形的性质求得∠AFE，∠BFE的度数，再根据三角形外角的性质即可求得答案.
解：∵∠CBA=90°，∠ABE=60°，
∴∠CBE=150°，
∵四边形ABCD为正方形，三角形ABE为等边三角形，
∴BC=BE，
∴∠BEC=15°，
∵∠FBE=∠DBA+∠ABE=105°，
∴∠BFE=60°，
在△CBF和△ABF中，
BF＝BF，∠CBF＝∠ABF，BC＝BA，
∴△CBF≌△ABF（SAS），
∴∠BAF=∠BCE=15°，
又∵∠ABF=45°，且∠AFD为△AFB的外角，
∴∠AFD=∠ABF+∠FAB=15°+45°=60°．
故答案为：60°
科目：初中数学 来源： 题型：
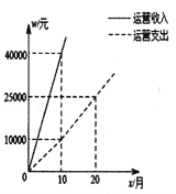
【题目】近年来，共享汽车的出现给人们的出行带来了便利，一辆
型共享汽车的先期成本为8万元，如图是其运营收入
(元)与运营支出
(元)关于运营时间
(月)的函数图象.其中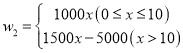
，一辆
型共享汽车的盈利
(元)关于运营时间(月)的函数解析式为
(1)根据以上信息填空：与的函数关系式为_________________；
(2)经测试，当
，共享汽车在这个范围内运营相对安全及效益较好，求当
，一辆型共享汽车的盈利
(元)关于运营时间(月)的函数关系式；(注：一辆共享汽车的盈利=运营收入-运营支出-先期成本)
(3)某运营公司有型，型两种共享汽车，请分析一辆型和一辆型汽车哪个盈利高；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两人参加某体育项目训练，为了便于研究，把最后5次的训练成绩分别用实线和虚线连接起来，如图，下面的结论错误的是（ ）
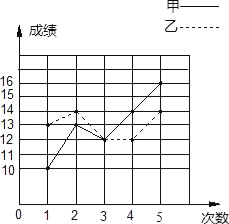
A. 乙的第2次成绩与第5次成绩相同
B. 第3次测试，甲的成绩与乙的成绩相同
C. 第4次测试，甲的成绩比乙的成绩多2分
D. 在5次测试中，甲的成绩都比乙的成绩高
查看答案和解析>>
科目：初中数学 来源： 题型：
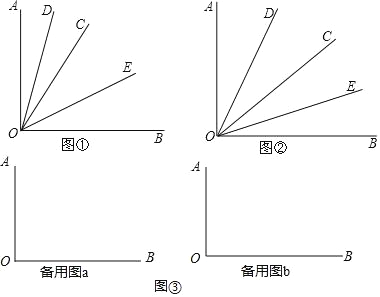
【题目】已知：∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD、OE．
（1）如图①，当∠BOC=70°时，求∠DOE的度数；
（2）如图②，若射线OC在∠AOB内部绕O点旋转，当∠BOC=α时，求∠DOE的度数.
（3）如图③，当射线OC在∠AOB外绕O点旋转时，画出图形，直接写出∠DOE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
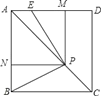
【题目】如图，已知正方形ABCD的边长为1，P是对角线AC上任意一点，E为AD上的点，且∠EPB=90°，PM⊥AD，PN⊥AB．
（1）求证：四边形PMAN是正方形；
（2）求证：EM=BN；
（3）若点P在线段AC上移动，其他不变，设PC=x，AE=y，求y关于x的解析式，并写出自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，A(－4，0)、B(2，0)，点C在y轴的正半轴上，且三角形ABC的面积为
．
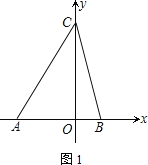
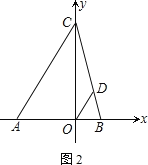
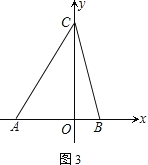
（1）求点C的坐标．
（2）过O点作OD平行于AC交CB于点D，问：x轴上是否存在一点P，使S△PBD＝
？若存在，求出点P的坐标；若不存在，请说明理由．
（3）若∠ACO＝30°，射线CA绕C点以每秒3°的速度逆时针旋转到CA′，射线OB绕O点以每秒10°的速度逆时针旋转到OB′．当OB转动一周时两者都停止运动．若两射线同时开始运动，在旋转过程中，经过多长时间，CA′∥OB′？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知函数y-
xb的图象与x轴、y轴分别交于点A、B，与函数yx的图象交于点M，点M的横坐标为2，在x轴上有一点Pa,0（其中a2），过点P作x轴的垂线，分别交函数yxb和yx的图象于点C、D.
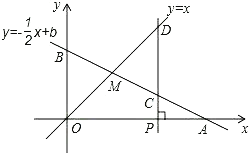
（1）求点M的坐标；
（2）求点A的坐标；
（3）若OBCD，求a的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图O是正五边形ABCDE的中心，OA=1．
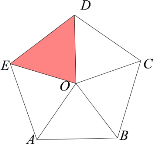
（1）△ODE绕着点 按 方向旋转 度，可以得到△OBC；
（2） △ODE沿 所在直线翻折，可以得到三角形 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
