
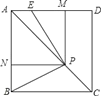
【题目】如图,已知正方形ABCD的边长为1,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
(1)求证:四边形PMAN是正方形;
(2)求证:EM=BN;
(3)若点P在线段AC上移动,其他不变,设PC=x,AE=y,求y关于x的解析式,并写出自变量x的取值范围.
【答案】(1)见解析;(2)见解析;(3)y=1-![]() (0≤x≤
(0≤x≤![]() ).
).
【解析】
(1)由四边形ABCD是正方形,易得∠BAD=90°,AC平分∠BAD,又由PM⊥AD,PN⊥AB,即可证得四边形PMAN是正方形;
(2)由四边形PMAN是正方形,易证得△EPM≌△BPN,即可证得:EM=BN;
(3)首先过P作PF⊥BC于F,易得△PCF是等腰直角三角形,继而证得△APM是等腰直角三角形,可得AP=![]() AM=
AM=![]() (AE+EM),继而求得答案.
(AE+EM),继而求得答案.
(1).∵正方形ABCD,
∴∠NAM=90.
又因为PM⊥AD,PN⊥AB,
∴∠ANP=∠AMP=90,
∴四边形PMAN是矩形(有三个角是直角).
∵P在AC上,
∴PM=PN(角平分线上的点到这条线段两边的距离相等),
∴四边形PMAN是正方形;
(2).∵∠EPB=90,
∴∠BPN+∠APN=90.
∵∠EPM=∠APN=90,
∴∠BPN=∠EPM,
在△BPN与△EPM中
∠BPN=∠EPM,PN=PM,∠BNP=∠EMP,
∴△BPN≌△EPM,
∴BN=EM;
(3)过P作PF⊥BC于F,如图所示:
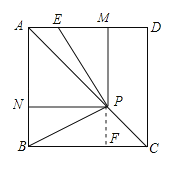
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC=1,∠PCF=45°,
∴AC=![]() ,△PCF是等腰直角三角形,
,△PCF是等腰直角三角形,
∴AP=AC-PC=![]() -x,BN=PF=
-x,BN=PF=![]() ,
,
∴EM=BN=![]() ,
,
∵∠PAM=45°,∠PMA=90°,
∴△APM是等腰直角三角形,
∴AP=![]() AM=
AM=![]() (AE+EM),
(AE+EM),
即![]() -x=
-x=![]() (y+
(y+![]() ),
),
解得:y=1-![]() x,
x,
∴x的取值范围为0≤x≤![]() ,
,
∴y=1-![]() x(0≤x≤
x(0≤x≤![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是面积为4![]() 的等边三角形,△ABC∽△ADE,
的等边三角形,△ABC∽△ADE,
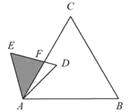
AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积
等于___(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过点A0,2的直线l1:y1kxbk0与直线l2:y2x1交于点P2,m。
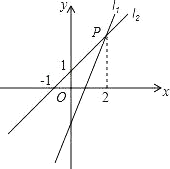
(1)求点P的坐标和直线l1的解析式;
(2)直接写出使得y1y2的x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点Pa,b和点Qa,b,给出如下定义:若![]() ,则称点Q为点P的限变点,例如:点(2,3)的限变点的坐标是(2,3),点2,5的限变点的坐标是2,5。
,则称点Q为点P的限变点,例如:点(2,3)的限变点的坐标是(2,3),点2,5的限变点的坐标是2,5。
(1)在点A2,1,B1,2中有一个点是函数y=![]() 图象上某一个点的限变点,这个点是 ;
图象上某一个点的限变点,这个点是 ;
(2)求点![]() ,1的限变点的坐标;
,1的限变点的坐标;
(3)若点P在函数yx32xk,k2的图象上,其限变点Q的纵坐标b的取值范围是5b2,求k的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ∥
∥![]() ,BE∥CF,BA⊥
,BE∥CF,BA⊥![]() ,DC⊥
,DC⊥![]() ,下面给出四个结论:①BE=CF;②AB=DC;③
,下面给出四个结论:①BE=CF;②AB=DC;③![]() ;
;
④四边形ABCD是矩形.其中说法正确的有( )
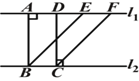
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com